Grundlagen der Physik I UE WS 2013/14

261 Technische Physik (Bac.) Grundlagen der Physik I
21

SG is die Ortsfunktion vom Geschoss und SZ die Ortsfunktion des herabfallenden Ziels.
hab das auch entdeckt, hat mir bei dem bespiel recht geholfen.

22

danke, jetzt wird mir die Sache auch klarer…!

23

lösungen 1-6
Epson_23102013181936.pdf (1.86 MB)

24

Neuer Thread…

25

Das Beispiel 2 steht genau gleich im Demtröder, Kapitel 2.7.2.

26

Hey, könnte mir jemand den angaben zettel hochladen?

27

die angaben findest du im tiss in den unterlagen der Grundlagen der Phyis I Übung

28

Seids bitte trotzdem so lieb und ladets es hoch. Danke :slight_smile:

29

Bittesehr :slight_smile:
ANG311013.pdf (32 KB)

30

Für die Rechenfaulen :slight_smile:

BSP 2 Punkt a und b :wink:


Cheers D
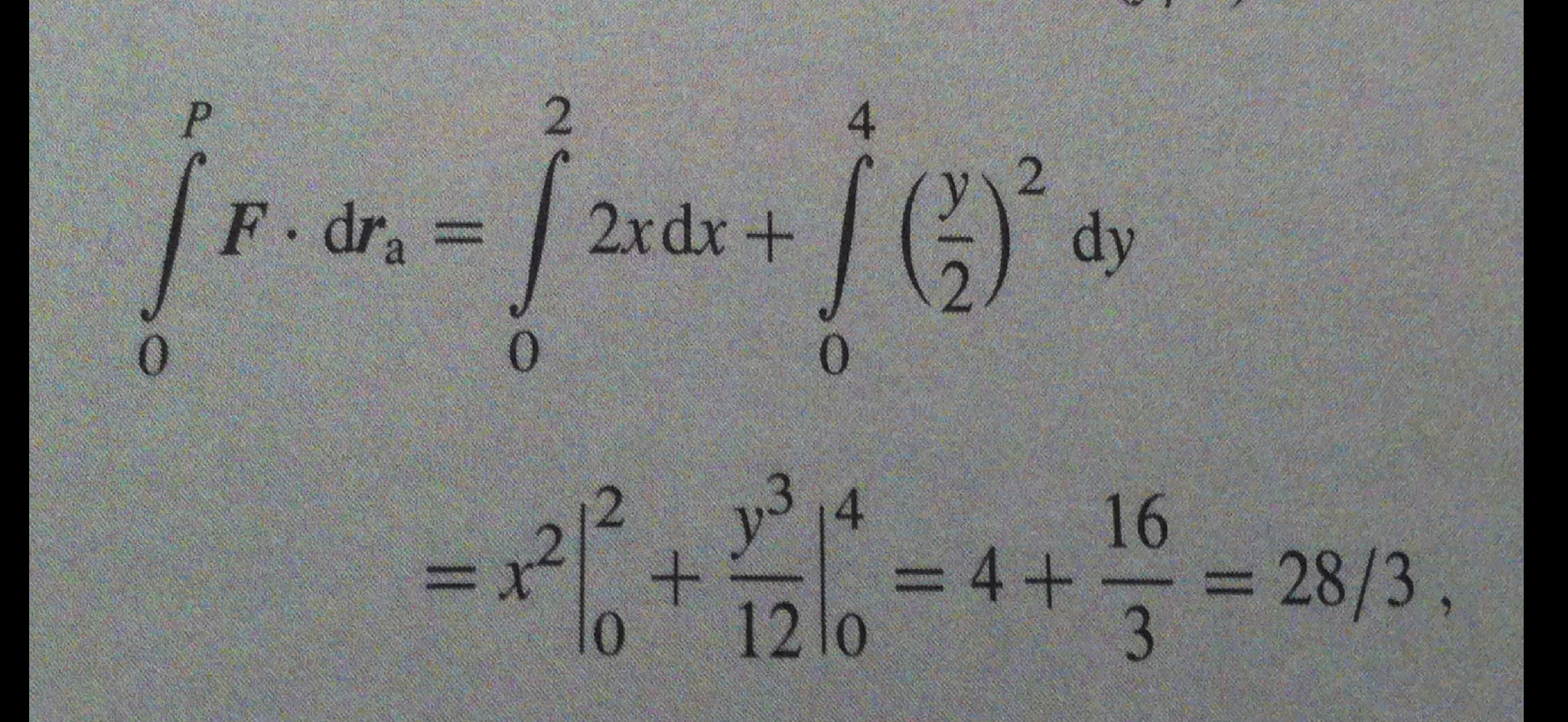
2.7.2B UEIV THP.png
2.7.2 UEIV TPH.png

31

1-5 6kommt morgen

sry falsche beisiele richtige siehe nächste seite

32

Mit welchem Abstand zum Mond habt ihr Beispiel 3 gerechnet?

33

wie kommst du beim ersten bsp auf 2x und (y/2)^2?

ich hab das anders gerechnet,
über kurvenintegrale mit einer parametrisierung!

34

aufgabe 6 is online
Epson_30102013113245.pdf (1.77 MB)

35

danke, sieht nach UE III aus, nicht UE IV

36

sieht nicht nur so aus :smiley:

na dann viel spass dir beim rechnen der richtigen beispiele bis morgen :stuck_out_tongue:

37

@ Myon:

Aus \vec{F}(\vec{r}_A_E)=-GmM_E/(r_A_E)^2 = -GmM_M/(r_A_M)^2=\vec{F}(\vec{r}_A_M)
und r_E_N_T_F = r_A_E+r_A_M

Erhält man
r_A_E=(r_E_N_T_F)/(\sqrt{M_m/M_E}+1)

Wobei
M_M…Mondmasse
M_E…Erdmasse
r_A_E…Abstand zur Erde beim Kräftegleichgewicht
r_A_M…Abstand zum Mond beim Kräftegleichgewicht
r_E_N_T_F…Abstand zwischen Erde und Mond

38

Meine Lösungen:
UE4LoesungWulfInside.pdf (3.26 MB)

39

richtige beispiele sry hab nicht geschaut nur gescannt und upgeloaded :slight_smile:
der upload da is aber auch scheiße hier der db link:

bsp 1-5 https://dl.dropboxusercontent.com/u/36087865/5.%20Übung.pdf
bsp 5 https://dl.dropboxusercontent.com/u/36087865/5.%20Übung%20bsp.6.pdf

40

=D>