da is ein diagramm zu nem ähnlichen beispiel. da sieht man relativ schön wie das zu lesen ist.
http://itp.nat.uni-magdeburg.de/~kassner/srt/pseudoparadoxa/stab_scheune/stab_scheune.html
Na dann danken wir der Sophie Seidenbecher dass Sie in der Schule schon so gescheit war 
Scheint auch was geworden zu sein aus ihr http://www.ioap.tu-berlin.de/menue/arbeitsgruppen/ag_dopfer/mitarbeiter/
Lg
ahhhhhhhhhh ausgezeichnet e-küsschen-schick…
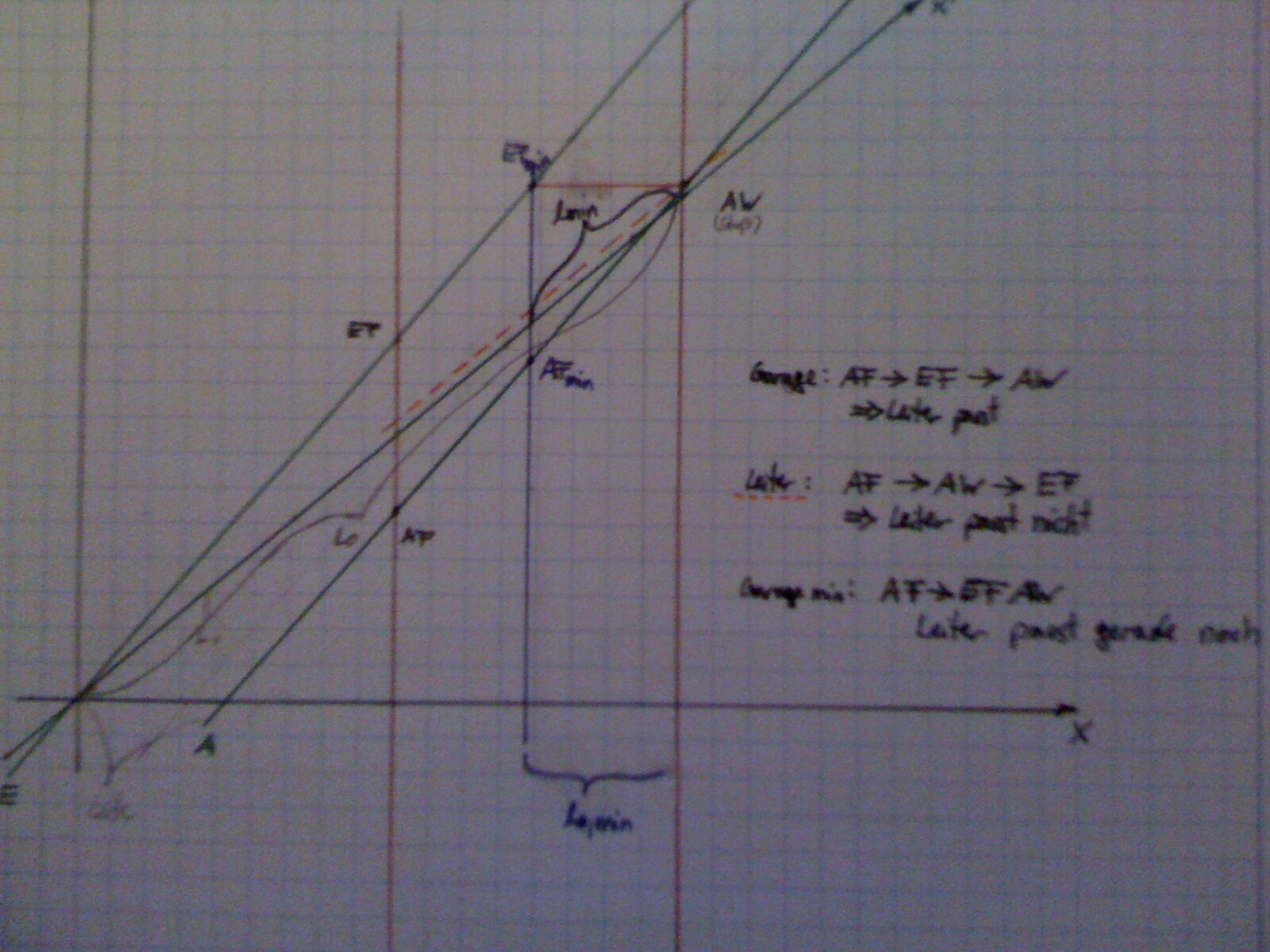
mich hat von anfang an verwirrt warum in der musterlösung das eine ende der leiter gleich auf der ct’ achse liegt… aber jetzt seh ich alles
dankööööööööö
gut… dann eins noch… wie trage ich l_{min} , l_{0,min} , wobei ich mich frage was ersteres sein soll, ein…
ich kann nur raten, und meine dass bei der musterlösung, vom schnittpunikt „ende-leite & hintere-wand“ normal richtung anfang-leiter gegangen wird… warum?
hoffe es hilft ist ein bischen anders als die musterlösung
Hier mal mein Minkowski zum ersten Bsp wobei ich Fuchs die zwei Inertialsystem genau umgekehrt angeordnet hab
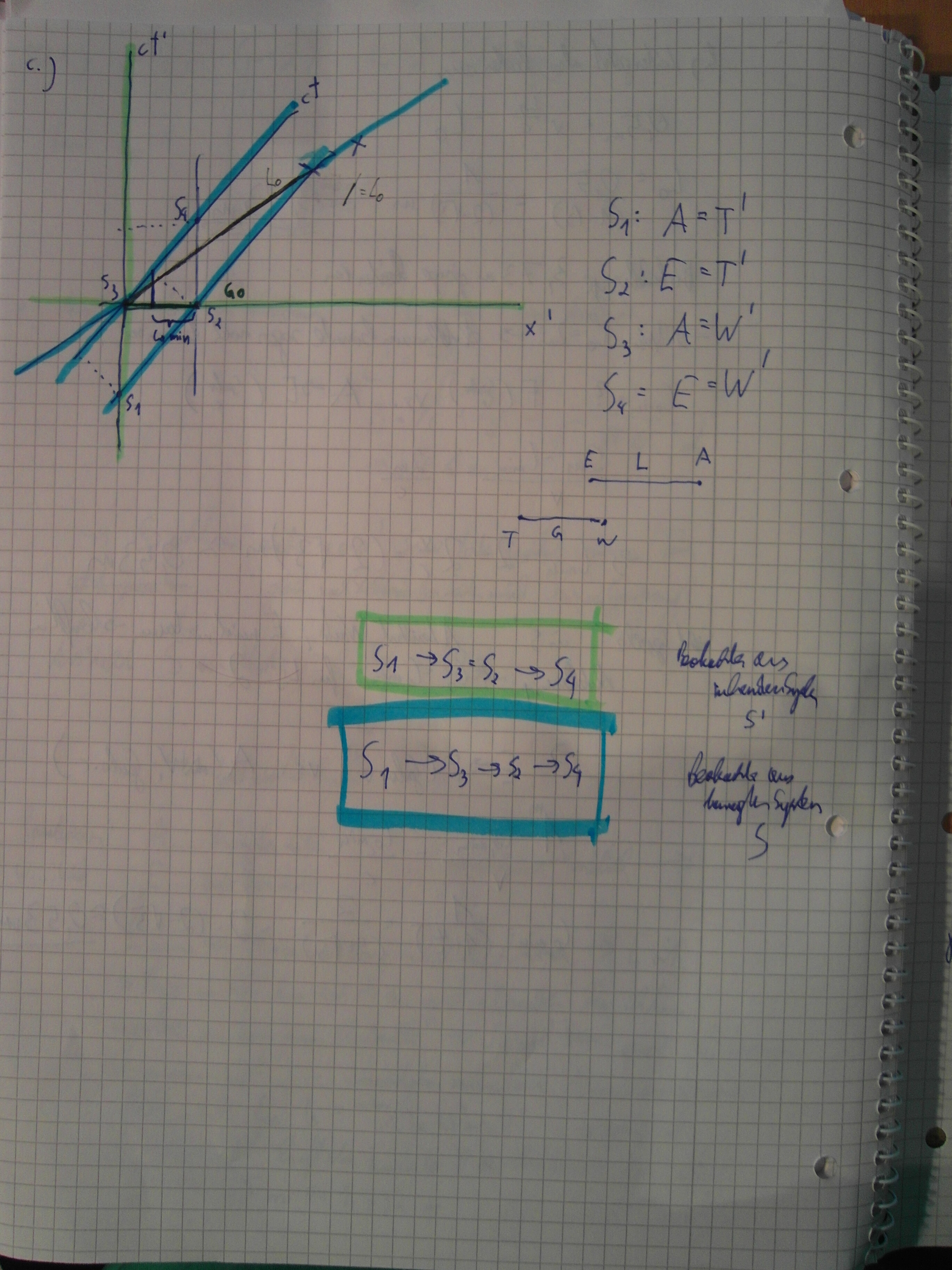
Und hat wer was zu 2 oder 3b!?
hmmm also du gehst waagrecht von AW zur E-weltlinie? und das is dann das l_0min? , projeziert auf die x-achse?
@chrisfresh… sorry, aber da erkennt ma gaaaaaaaaaaaaaaaar nix 
edit: was fehlt dir bei 3b) ?
edit2: und wie kommt die gestrichelte linie zustande, meiner meinung nach is die zu nix paralell
@Chrisisfresh dank deiner skizze bin ich draufgekommen das ich die achsen falsch beschriftet habe danke =D>
@stan-ii meine gestrichelte linie ist paralllel zu x`(bzw nach änderung x) Achse falls du mich gemind hast
und l_0min sollte meiner meinung nach das sein, weill das ist ja genau dann wenn die leiter an der wand anstoßt und gleichzeitig ganz im abstellraum ist
thx, daumen-hoch
zu 3b)
du musst nur stur matrizen multiplizieren und dann verwenden, dass \sin x ; \sin y = \frac{1}{2}\Big(\cos (x-y) - \cos (x+y)\Big)
\cos x ; \cos y = \frac{1}{2}\Big(\cos (x-y) + \cos (x+y)\Big)
\sin x ; \cos y = \frac{1}{2}\Big(\sin (x-y) + \sin (x+y)\Big)
wobei halt x=\alpha und y=\alpha ’
wenn man die endmatrix mit der vergleicht die rauskommen soll is ganz klar dass \alpha= \frac{\Pi}{2} und \alpha '= - \frac{\Pi}{2}
da ja \sin(\pm\frac{\Pi}{2})=\pm 1 \cos(\pm\frac{\Pi}{2})=0
dass die drehwinkel \pm \frac{\Pi}{2} sein müssen is außerdem auch logisch weil man sich ja um die achsen dreht und nur die lorentztrafo in zrichtung anhand der in x-richtung darstellen will. ist so als wenn du immer nur vorwärtsschritte gehen kannst aber auf die seite musst ^^
@2)
ich hab http://homepage.univie.ac.at/franz.embacher/SRT/Geschwindigkeitsaddition.html gefunden. es geht um geschwindigkeitsaddition und passt wohl zu unserem bsp 2
vl hilfts ja auch sonst noch wem…
Wie Khalida schon gesagt hat ist 10.3 eigentlich nicht so schwer wie es aussieht.
Für 10.3 a) multipliziert man die Drehmatrix mit dem 4er-Vektor, dann geht man nach dem Schema aus dem Vorlesungsfolien vor indem man jede Komponente des neuen 4er-Vektors „s“ quadriert und von einander abzieht. Also s^2=(…)^2-x^2-y^2-(…)^2, wobei die Klammern die einzig interessanten Ausdrücke bringen. Dann hebt man (ct)^2 und z^2 heraus und kommt auf eine Form die man durch Umformung (die Klammerausdrücke Gamma^2-Gamma^2*Beta^2 = 1) auf eine Form (ct)^2 - x^2 - y^2 - z^2 = s^2. Damit hat man das schon Bewiesen
Für 10.3 b) schreibt man einfach die drei Matrizen auf (eine steht z.B. in den VO-Folien), und führt ganz einfach die Matrixmultiplikation von links nach rechts durch. Dann kommt man auf ein paar Gleichungen wo man ganz einfach sieht welche werte cos(alpha) haben muss damit diese Stelle der Matrix =0 ist.