Auf die Plätze… fertig… Los!
Viel Motivation bei der letzten Übung 
tutorium10_angabe.pdf (49.4 KB)
Ich schreibe mal meine Lösungen für die Multiple Choice Fragen auf:
a)
|(ix-\frac{1}{2})!|^2=|\Gamma{(ix+\frac{1}{2})}|^2 mit der Identität: z!=\Gamma{(z+1)}
weiters |\Gamma{(ix+\frac{1}{2})}|^2=\Gamma{(\frac{1}{2}+ix)}\Gamma{(\frac{1}{2}-ix)}
Jetzt benutzen wir die Identität \Gamma(z)\Gamma(1-z)=\frac{\pi}{sin(\pi z)} aus der Angabe und kommen mit z=\frac{1}{2}-ixauf:
\Gamma{(\frac{1}{2}+ix)}\Gamma{(\frac{1}{2}-ix)}=\frac{\pi}{sin(\pi(\frac{1}{2}-ix))}=\frac{\pi}{cos(i\pi x)}=\frac{\pi}{cosh(\pi x)}
b)
|e^{-\frac{\pi \gamma}{2}}\Gamma(1+i\gamma)|^2=e^{-\pi\gamma}|\Gamma(1+i\gamma)|^2 weil e^{-\pi\gamma}>0 für alle \gamma
Den Betrag zerlegen wir wie vorher und erhalten: e^{-\pi\gamma} \Gamma(1+i\gamma)\Gamma(1-i\gamma)
Jetzt benützen wir die angegebene Identität \Gamma(1+z)=z\Gamma(z)
und kommen auf e^{-\pi\gamma}i\gamma \Gamma(i\gamma)\Gamma(1-i\gamma)
Darauf können wir wieder die Identität aus a) anwenden mit z=i\gamma und kommen auf:
\frac{e^{-\pi\gamma}i\gamma\pi}{\sin(i\pi\gamma)}=\frac{i\gamma\pi}{e^{\pi\gamma}\sin(i\pi\gamma)}=\frac{\gamma\pi}{e^{\pi\gamma}\sinh(\pi\gamma)}=\pi\gamma(coth(\pi\gamma)-1)=\frac{2\pi\gamma}{e^{2\pi\gamma}-1}
c)
\Gamma(\frac{1}{2}-n)\Gamma(\frac{1}{2}+n)
Für dieses Beispiel müssen wir zuerst \Gamma(\frac{1}{2}+n) wie folgt umformen.
\Gamma(n+\frac{1}{2})=\frac{2n-1}{2}\Gamma(n-\frac{1}{2})=\frac{2n-1}{2}\frac{2n-3}{2}\Gamma(n-\frac{3}{2})=\frac{2n-1}{2}\frac{2n-3}{2}\frac{2n-5}{2}\Gamma(n-\frac{5}{2})=…=\frac{2n-1}{2}\frac{2n-3}{2}\frac{2n-5}{2}…\frac{1}{2}\Gamma(\frac{1}{2})=\frac{(2n-1)!!}{2^n}\sqrt{\pi}
Es gilt: (2n-1)!!=\frac{(2n)!}{2^n \cdot k!}
\frac{(2n-1)!!}{2^n}\sqrt{\pi} lässt sich also schreiben als \frac{(2n)!}{n! \cdot 4^n}\sqrt{\pi}
Für \Gamma(\frac{1}{2}-n) kommt man auf \frac{n! \cdot (-4^n)}{(2n)!}\sqrt{\pi}
Das heißt: \Gamma(\frac{1}{2}-n)\Gamma(\frac{1}{2}+n)=\pi \frac{n! \cdot (-4^n)}{(2n)!}\cdot \frac{(2n)!}{n! \cdot 4^n}=(-1)^n\pi
Alternativ, wahrscheinlich schneller:
Es gibt auch die Möglichkeit einfach den Hinweis \Gamma(z)\Gamma(1-z)=\frac{\pi}{sin(\pi z)} anzuwenden mit z=\frac{1}{2}-n
Dann kommt man auf \Gamma(z)\Gamma(1-z)=\frac{\pi}{sin(\pi z)}=\frac{\pi}{sin(\pi (\frac{1}{2}-n))} und wenn man dann für n nur Ganze Zahlen betrachtet kommt man auf das selbe weil ja sin(\pi (\frac{1}{2}-n))=(-1)^n. Dieser Weg ist vielleicht leichter nachvollziehbar
d)
\int_{-\infty}^{\infty}x^{2a}e^{-x^2}dx
Für dieses Beispiel brauchen wir den Hinweis: \Gamma(z)=\int_0^{\infty}t^{z-1}e^{-t}dt
Wir substituieren x aus \int_{-\infty}^{\infty}x^{2a}e^{-x^2}dx mit: t=x^2 und dt=2xdx \rightarrow x=\sqrt{t} Die Funktion von t ist jetzt gerade und für x\rightarrow -\infty geht t\rightarrow \infty
Deshalb schreibe ich das Substituierte Integral *2 und mit den Grenzen von 0 bis \infty
Man erhält: 2\int_{0}^{\infty}t^{a}e^{-t}\frac{1}{2\sqrt{t}}dt
2\int_{0}^{\infty}t^{a}e^{-t}\frac{1}{2\sqrt{t}}dt=\int_{0}^{\infty}\frac{t^{a}}{\sqrt{t}}e^{-t}dt=\int_{0}^{\infty}t^{a+\frac{1}{2}-1}e^{-t}dt=\int_{0}^{\infty}t^{a-\frac{1}{2}}e^{-t}dt=\Gamma(a+\frac{1}{2})
e,f folgt im nächsten Post, weil der Computer bei so viel Latex so langsam wird, und falls jemand Fehler findet bitte melden 
e)
Korrigierte Version!
-\int_0^1x^aln(x)dx
Ich bin das Beispiel mit der normalen Partiellen Integration angegangen mit:
\int fg’=fg-\int f’g
sowie: f=ln(x), f’=\frac{1}{x}, g=\frac{x^{a+1}}{a+1}, g’=x^{a}
Eingesetzt in die Formel und ich komme auf:
-(\frac{x^{a+1}}{a+1} ln(x)|_0^1-\int_0^1\frac{x^{a+1}}{x(a+1)}dx)=-(0-\int_0^1\frac{x^{a}}{(a+1)}dx)=\frac{x^{a+1}}{(a+1)^2}|_0^1=\frac{1}{(a+1)^2}
f)
\int_0^\infty e^{-x^4}dx
Bei diesem Beispiel substituiere ich wieder und zwar: t=x^4, dt=4x^3dx, \rightarrow x=\sqrt[4]{t}, \rightarrow dx=\frac{dt}{4\sqrt[4]{t^3}, Die Grenzen bleiben gleich.
Man kommt also auf: \int_0^\infty e^{-t}\frac{dt}{4\sqrt[4]{t^3}}=\frac{1}{4}\int_0^\infty \frac{e^{-t}}{t^{\frac{3}{4}}}dt=\frac{1}{4}\int_0^\infty t^{-\frac{3}{4}}e^{-t}dt
Das wird jetzt mit der Identität \Gamma(z)=\int_0^\infty t^{z-1}e^{-t}dt und z=\frac{1}{4}
\frac{1}{4}\int_0^\infty t^{-\frac{3}{4}}e^{-t}dt=\frac{1}{4} \Gamma(\frac{1}{4})=\Gamma(\frac{5}{4})=\frac{1}{4}!=0,9064024770554770779826712889…
Also nochmal, falls wer Fehler findet bitte sagen, und alle Angaben ohne Gewähr.
Hat jemand schon was zu 10.2) oder 10.3) wäre dankbar!
lg
gwd, du hast den Fehler beim partiellen integration,bei der Funktion g=1/x und dann g’=lnx…das ist umgekehrt…
g=lnx dann g’=1/x dann kommst du auf die richtige lösung
Hätte jemand vielleicht Idee zur Aufgabe 3 a,b,c ?
Bei 3, d ist mir nur ein Schritt unklar:
natürlich hast recht, danke - habe es schon korrigiert.
3a hab ich, kann ich später posten aber beim Rest bin ich noch ratlos
gwd, wie machst du die Umformungen bei 1c?
c)
\Gamma(\frac{1}{2}-n)\Gamma(\frac{1}{2}+n)
Für dieses Beispiel müssen wir zuerst \Gamma(\frac{1}{2}+n) wie folgt umformen.
\Gamma(n+\frac{1}{2})=\frac{2n-1}{2}\Gamma(n-\frac{1}{2})=\frac{2n-1}{2}\frac{2n-3}{2}\Gamma(n-\frac{3}{2})=\frac{2n-1}{2}\frac{2n-3}{2}\frac{2n-5}{2}\Gamma(n-\frac{5}{2})=…=\frac{2n-1}{2}\frac{2n-3}{2}\frac{2n-5}{2}…\frac{1}{2}\Gamma(\frac{1}{2})=\frac{(2n-1)!!}{2^n}\sqrt{\pi}
Blöde Frage - ist das das letzte Tutorium? Oder gibts noch eins nach dem Test?
meine Variante von 1c wäre anders:
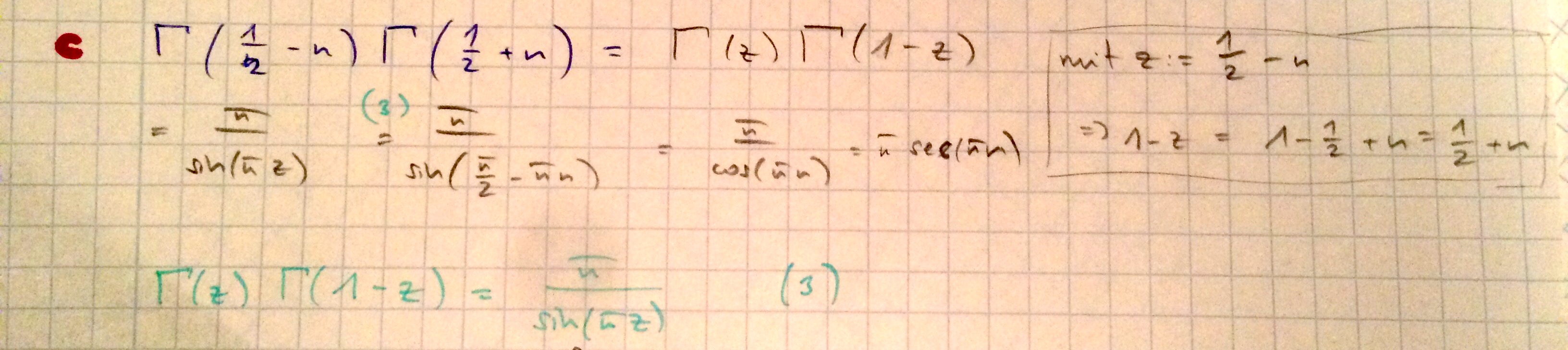
Naja in den Hinweisen steht ja z!=\Gamma(z+1), daraus folgen diese Umformungen.
Danke für die Info!
Ja das ist auch möglich, allerdings solltest du dann noch berücksichtigen, dass n ja keine reelle Zahl, sondern nur eine Ganze Zahl ist, also aus dem Sinus wird dann ein (-1)^n Ich hab deine Variante jetzt auch in meinem Posting oben dazugeschrieben.
Das ist das letzte Tutorium.
Darf man e.) überhaupt so „einfach rechnen“, ln(x) ist ja an der Stelle null nicht definiert wo ich aber das Integral auswerte?
Finde es auch verdächtig das keiner der Hinweise für diesen Punkt verwendet werden muss, Ergebnis scheint ja mit Wolfram Alpha überein zustimmen.
Ich bin mir auch nicht sicher, habe aber keine bessere Idee. Man kann das Ergebnis auch in der Form ankreuzeln.
10.3) a)
\nabla x^i=\frac{1}{g_{ii}}e_i
Nabla in Kugelkoordinaten: \nabla=e_r \frac{\partial}{\partial r}+\frac{1}{r}e_\theta \frac{\partial}{\partial \theta}+\frac{1}{r sin(\theta)}e_\phi \frac{\partial}{\partial \phi}
(x^1,x^2,x^3)=(r,\theta ,\phi)
Definition der Kugelkoordinaten:
x=rsin(\theta)cos(\phi)
y=rsin(\theta)sin(\phi)
z=rcos(\theta)
dx=dx^ie_i
e_i’=\frac{dx^i}{dx’^j}e_j
e_{ki} sind die Kartesischen Basisvektoren.
e’1=e{k1}sin(\theta)cos(\phi)+e_{k2}sin(\theta)sin(\phi)+e_{k3}cos(\theta)
e’2=e{k1}rcos(\theta)cos(\phi)+e_{k2}rcos(\theta)sin(\phi)-e_{k3}rsin(\theta)
e’3=e{k1}(-rsin(\theta)sin(\phi))+e_{k2}rsin(\theta)cos(\phi)+e_{k3}*0
g_{11}=e’_1 \cdot e’1
g{22}=e’_2 \cdot e’2
g{33}=e’_3 \cdot e’_3
g_{ij}=\begin{pmatrix}{1}&{0}&0\{0}&{r^2}&{0}\{0}&0&{r^2sin^2\theta} \end{pmatrix}
zu beachten für Nabla:
e_r=\frac{e_1’}{|e_1’|}
e_\theta=\frac{e_2’}{|e_2’|}
e_\phi=\frac{e_3’}{|e_3’|}
mit |e_1’|=1 |e_2’|=r |e_3’|=rsin(\theta)
einsetzen in die Angabe:
\nabla x^1=e_r \frac{\partial r}{\partial r}+\frac{1}{r}e_\theta \frac{\partial r}{\partial \theta}+\frac{1}{r sin(\theta)}e_\phi \frac{\partial r}{\partial \phi}
\nabla x^2=e_r \frac{\partial \theta}{\partial r}+\frac{1}{r}e_\theta \frac{\partial \theta}{\partial \theta}+\frac{1}{r sin(\theta)}e_\phi \frac{\partial \theta}{\partial \phi}
\nabla x^3=e_r \frac{\partial \phi}{\partial r}+\frac{1}{r}e_\theta \frac{\partial \phi}{\partial \theta}+\frac{1}{r sin(\theta)}e_\phi \frac{\partial \phi}{\partial \phi}
bei uns: e_i’=e_i aus der Angabe.
\frac{1}{g_{ii}}e_i ist trivial und man sieht, dass beide Seiten das gleiche ergeben.
10.3) b)
\nabla \cdot (\frac{1}{G}e_i)=0 mit G=\sqrt{g_{11}g_{22}g_{33}}
Es gilt: e_1=ae_2\times e_3 und \nabla \cdot (A \times B)=(\nabla \times A) \cdot B - A \cdot (\nabla \times B) und \nabla \times (\nabla b)=0
wir wissen:
\nabla x^i=\frac{1}{g_{ii}}e_i
\rightarrow e_i=\nabla x^i g_{ii}
\nabla \cdot (\frac{1}{G} a e_2 \times e_3)=\nabla \cdot (\tilde{e}_2 \times e_3)
\tilde{e}_2=\frac{1}{G} a e_2
(\nabla \times \tilde{e}_2)\cdot e_3-\tilde{e}2 \cdot (\nabla \times e_3)= (\nabla \times (\nabla x^2 \frac{a g{22}}{G})) \cdot e_3-\tilde{e}2 \cdot (\nabla \times (\nabla x^3 g{33}))
mit \nabla \times (\nabla x^2 \frac{a g_{22}}{G})=0 und \nabla \times (\nabla x^3 g_{33})=0
Bin mir nicht sicher bei beiden Beispielen, wenn jemand alternative Vorschläge hat / Fehler findet, bitte mitteilen
Wie kommt man auf diese Identität? Habe ich weder im Buch noch in der Angabe gefunden
So wie bei komplexen Zahlen allgemein |z|^2=z \cdot \bar{z} mit \bar{z} ist die konjungiert komplexe Zahl.
Dass das mit der Gammafunktion genauso geht hab ich auf higgs.at irgendwo gesehen in den Lösungen der letzten Jahre.
Okay, das war das was mir unklar war. Hab noch ein bisschen gegoogelt, siehe das Lemma 2.5 hier:
http://uni.robinlang.net/wp-content/uploads/2013/06/skript.pdf
hat nicht vielleicht jemand 3c)d) vollständig? 
Ich bekomme 1/2a beim 1.e
Hat das 10.2 überhaupt irgendwer gerechnet?
@GWD
Bei deinem 3.b) gehört glaub ich der Faktor a ab der vorletzten Zeile in den Zähler. Ändert aber eh nichts an der Lösung.
Hab das 2er leider auch nicht… Hat vielleicht wer 3.e) vollständig?
Hoffentlich bald gute Nacht