Die Angabe ist schon online, welch eine Freude! Runterladen muss aber für dieses Jahr mal reichen ![]()
tut2009_11.pdf (68 KB)
hmm… naja mal schaun… ![]()
Bevor ich über die Ferien noch alles Quantenzeugs vergesse, hier mal meine Vorschläge:
1a) \alpha=\frac{1}{\sqrt 3},\ |\psi>=\frac{1}{\sqrt 3}(|211> + (1-i)|2 1 -1>)
1b)
1.Die normierten Eigenzustände von Lx in jene von Lz entwickeln (aus Bsp1 10.Tut):
|\hbar->=\frac{1}{2}(|2 1 -1> -\sqrt{2}|2 1 0> + |2 1 1>)\
|\hbar_0>=\frac{1}{\sqrt 2}(|2 1 -1> -|2 1 1>)\
|\hbar+>=\frac{1}{2}(|2 1 -1> + \sqrt{2}|2 1 0> + |2 1 1>)
2.
P(Lx= \hbar +)=|<\hbar+|\psi>|^2=\frac{5}{12}\
P(Lx=\hbar_0)=\ldots=\frac{2}{12}\
P(Lx=\hbar-)=\ldots=\frac{5}{12}\
\
\Rightarrow\ =0
1c)P(Lz=-\hbar){|\psi>}=\frac{2}{3}
nach dieser Messung kollabiert Psi: |\psi>\rightarrow |\psi’>=|2 1 -1>
Für Messung von Lx=h, |2 1 -1> in Eigenbasis von Lx entwickeln (mit 1b):
|2 1 -1>=\frac{1}{2}(|\hbar-> + \sqrt{2}|\hbar_0> + |\hbar+>)
P(Lx=\hbar){|2 1 -1>}=\frac{1}{4}\
\Rightarrow P({Lx,Lz}={\hbar,-\hbar})=P(Lz=-\hbar){|\psi>} . P(Lx=\hbar){|21-1>}=\frac{1}{6}
1d) Lx,Lz kommutieren nicht, d.h. es kommt auf Reihenfolge von Messung an, sieht man auch wenn man explizit nachrechnet. Wird wahrscheinlich schon als Begründung genügen.
Man könnte aber auch für Lx.Lz, Lz.Lx die Projektoren für {h,-h} anschreiben und zeigen, dass |\hbar+><\hbar+|.|2 1 -1><2 1 -1| \ne |2 1 -1><2 1 -1|.|\hbar+><\hbar+|
2)geg. \hat{H} \propto \vec{B}.\vec{S},\ \vec{B}=(0,0,B_z)\
\Rightarrow \hat{H}=2\alpha . Bz.\hat{S_z} (2.alpha ist der Proportionalitätsfaktor)
2a)
Um Zeitentwicklung von Psi(t=0) zu erhalten H in Eigenbasis von Sz darstellen
|\psi(t)>=U(t)|\psi_0>=\frac{1}{\sqrt 2}(e^{-i \alpha B_z t}|+> + e^{i \alpha B_z t}|->)
2b) Eigenzustände von Sz in Eigenzustände von Sx entwickeln:
|+>=\frac{1}{\sqrt 2}(|x+> + |x->)\
|->=\frac{1}{\sqrt 2}(|x+> - |x->)\
\
\
\Rightarrow\ |\psi(t)>=\cos(\alpha B_z t)|x+> - i.\sin(\alpha B_z t) |x->\
\Rightarrow\ P(Sx=\frac{\hbar}{2})_{|\psi(t)>}=\cos^2(\alpha B_z t)
2c) geg. \vec{B}=(B_x, 0,0)\ \Rightarrow\ \hat{H}=2 \alpha.Bx.\hat{S_x}
1.Psi(t=0) nach Eigenbasis von Sx entwickeln: |\psi_0>=|x+>
2.
|\psi(t)>=U|\psi_0>=e^{-i\alpha B_x t}|x+>\
\Rightarrow\ P(S_x=\frac{\hbar}{2})=1
3a-c) ist ein Standardbsp und steht wohl in jedem Lehrbuch (z.b. Cohen-Tannoudji, Quantum mechanics Band2 S.1018-1020) und sicher auch im Grau…
3a) {|–>,|-+>,|±>,|++>}
3b){|S M>}={|00>,|1-1>,|10>,|11>}
3c)
|11>=|++>\
|10>=\frac{1}{sqrt 2}(|±> + |-+>)\
|1-1>=|–>\
|00>=\frac{1}{sqrt 2}(|±> - |-+>)\
3d) geg.: \hat{H}{SS} \propto \vec{S_1}.\vec{S_2}\ \Leftrightarrow\ \hat{H}{SS}=\frac{2 \alpha}{\hbar^2} \vec{S_1}.\vec{S_2}
Es ist nun die Spin-Spin-WW für die Basiszustände der Gesamtdrehimpuls-Basis |S M> gefragt.
dazu verwendet man: \vec{S}=\vec{S_1}+\vec{S_2}\ \Rightarrow\ S^2=S_1^2+S_2^2 + 2\vec{S_1}.\vec{S_2}\
\Rightarrow\ \vec{S_1}.\vec{S_2}=\frac{1}{2}(S^2-S_1^2-S_2^2)
Weiters gilt bei Spin-1/2-Teilchen:
S_1^2=S_2^2=\hbar^2 \frac{3}{4}\
\
\
\Rightarrow \hat{H}_{SS} = \alpha(\frac{S^2}{\hbar^2}-\frac{3}{2})
Man erhält dann:
\hat{H}_{SS}=\frac{\alpha}{2}\begin{cases}
1 & , |1-1>,|10>,|11> \
-3& , |00>
\end{cases}
Hi!
…ich verstehe noch nicht ganz was du bei 1b machst! Ich dachte die bra und ket schreibweise ist Basislos!
Was ich von der 10.Übung mitnehme, ist dass die Quantenzahlen unabhängig von den einzelnen Basen ist!?
…bitte kläre mich auf!
- Bra-ket Schreibweise ist basisunabhängig, deswegen wird ja alles als Linearkombination der Kets (Basiszustände) angegeben…
- Die Quantenzahlen sind basisunabhängig (außer Die Projektionszahl). Die Eigenwerte der Drehimpulsprojektions(-matrizen) sind auch basisunabhängig (Argument war eben Isotropie des Raumes). Trotzdem unterscheiden sich die Matrizen, (es ist eben diesselbe Jordan-Normalform in unterschiedlichen Basen).
Da wir die Zustände aber in der Form |N L Lz> gegeben haben, wir in 1b) aber an der Wahrschl. den Eigenzustand h+ von Lx zu messen interessiert sind, müssen wir den Zustand in die Eigenbasis von Lx entwickeln: |N L Lx>.
Dann kann man wieder wie gewohnt über das Betragsquadrat des Koeff. von |2 1 1> die Wahrschl. für dessen Messung erhalten…
Hallo!
Ich habe eine Frage zu 1.d!
Wenn ich die Reihenfolge der Messungen umdrehe, wie kann man dann den Kollaps der Wellenfunktion verstehen?
Ersätze ich dann die ganze Zustandsfunktion durch die Eigenfunktion h+ von Lx?!
Die übrigen Ergebnisse von 1 bestätige ich!
Die Ergebnisse von Bsp 2 kann ich auch bestätigen!..bzw. erhalte ich die selben wie sie oben stehen!
Wenn du Lz.Lx |\psi> misst ersetzt du
- Ersetzt du Psi durch die EF für h+ von Lx (Kollaps).
Um die Wahrschl. für dessen Messung zu erhalten, musst du aber Psi in Lx entwickeln bzw. wenn du die EF für h+ von Lx durch |h+> bereits in Lz entwickelt hast und normiert ist (wie bei mir oben) einfach
|<h+|\psi>|^2 berechnen.
2.Danach muss |h+> (EF für h+ von Lx) durch die EF für -h von Lz ersetzt werden (Kollaps).
Die Wahrschl. für dessen Messung analog zu 1.
Für die Messung von Lx.Lz |\psi>
Vertausche in den obigen Punkten einfach Lx mit Lz…
Danke!
Wie ist die Frage 3c) gedacht? Sollen wir einfach die Koeffizienten mit einer Formel ausrechen (zB auf Seite 507 in [Grau]), oder stellen die sich irgendetwas anderes darunter vor (Leiteroperatoren)?
Hi!
Also ich habe 3c mit den Leiteroperatoren ausgerechnet…bin aber nicht besonders glücklich darüber, weil das sehr lange ist!
Wenn du etwas kürzeres findest dann sag bescheid! 3abc steht eigentlich so im Skriptum vom burgdörfer;)…
Beispiele 1 und 2 habe ich gelöst, aber das 3te (zumindest abc) ist seltsam. Diese Zustandsvektoren von a b kann man sich noch irgendwie vom Skript einreden lassen, aber eine vernünftige Methode die Linearkombinationen zu berechnen fällt mir momentan nicht ein und es findet sich auch nirgends etwas. Im Burgdörfer wirft er seitenlang mit irgend ner Drehung um sich und im Kreuzer Skript wird einfach so n Leiteroperator hingesetzt mit nem Vorfaktor. Weiß da momentan nicht weiter.
Mit der Bestimmung der |00> koeffizienten habe ich noch etwas probleme.
ich habe jetzt einen Leiteroperator angesetzt (die z-Komponenten):
S_{-}=S_{1-}+S_{2-}
und auf den Ansatz mit der linearkombination wirken lassen:
S_{-}|00>=(S_{1-}+S_{2-})(a|±>+b|-+>)
Da es für |00> keine „Leiter“ gibt wird die linke Seite 0 und rechts bekomme ich (Wirkungsquantuum schon raus gekürzt):
a|–>+b|–>=0
daher a+b=0
war mir zusammen mit der normierung a^2+b^2=1 die richtige Lösung liefert. Die Frage ist nur ob man es auch so machen darf oder nicht. Jemand ne Ahnung?
Sind diesmal viele Zettel, aber nur weil zwischendurch immer vieles durchgestrichen ist.





durchgestrichenes oder ausgeklammertes einfach ignorieren





seit methoden hab ich einfach keine lust mehr alles nochmal zu schreiben wenn ich mich irgendwo verrechnet habe. ausserdem is ein bisschen erinnerung dran wie man das beispiel gelöst hat ganz praktisch.



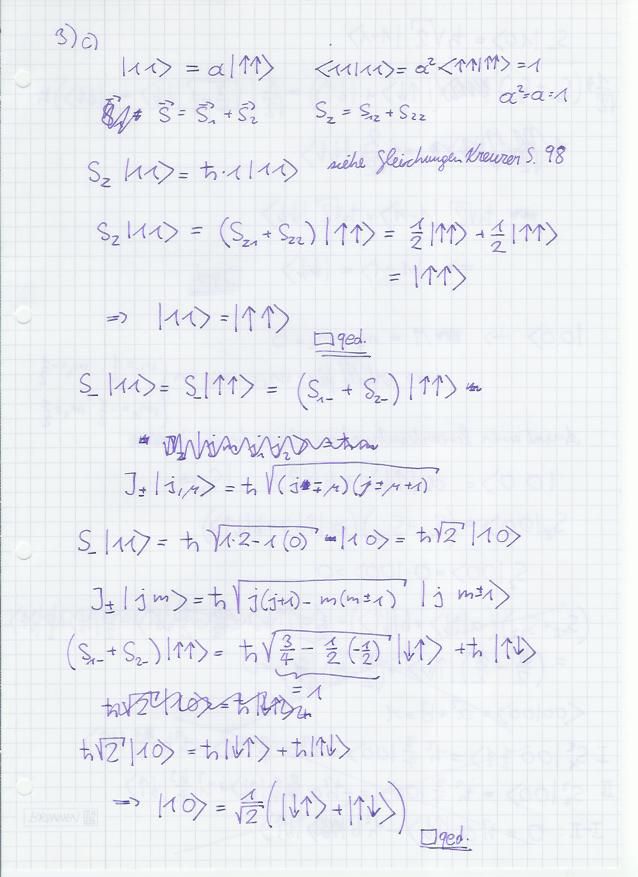
so ich habs noch gach ein bisschen download und druckerfreundlicher aufgearbeitet
übung11.pdf (896 KB)
Danke fürs online stellen und das hübsche zusammenfassen in ein PDF ![]()
Thx a lot
i glaub ja, dass wir alle miteinander dem lelouch was schulden für das semester, oder?