Ich habe einmal eine kleine mathematische formelsammlung zusammengestellt und dachte mir ich teile sie mal mit euch
Mathematische Formelsammlung.pdf (113 KB)
wenn jemandem noch etwas einfällt was ich vergessen habe bzw was man noch hinzufügen könnte bitte mitteilen
ich werde auch eventuell eine formelsammlung mit den für die übungen benötigten edyn formeln zusammenstellen und kann die dann auch hier hochladen falls interesse besteht
meine frage ist auch ob man auch die allgemeinen lösungen der laplace gleichung und die legendre-polynome in einer mathematischen formelsammlung verwenden darf?
zu wellen haben wir dieses semester ja nichts gemacht also ist das 2te beispiel vom 2009er test irrelevant oder? welche weiteren möglichen theoriefragen außer den beiden vom 2011er test gibt es denn eurer meinung noch? (war leider in letzter zeit nicht mehr so oft in der vo von daher bin ich leider nicht so gut informiert)
schwer zu sagen was noch so an theorei kommen kann da ich nicht weiß wie weit die vorlesung in den letzten jahren gekommen ist. aber da wir glaub ich ein bischen hintennach sind könnt ich mir noch vorstellen das er was zu elektrostatik mit dielektrika frag, dazu fehld mir aber die theorei hab da nur formel ohen Herleitung (falls es die überhaupt gibt).
Andererseits sind bei 1. Test auch genau die gleichen fragen gekommen 
.
hätte da auch noch n paar formeln, vlt hilfts ja wem … viel spaß damit
test_2.pdf (125 KB)
Bsp 4 von 2011! Es kann sein das sich Rechenfehler eingeschlichen haben aber vom Prinzip sollte es passen!hat jemand eine Idee zu Bsp 3 b und c von 2011?
könnte eventuell jmd die angabe vom 2011er test hochladen/abtippen (at least bsp 3&4) … finde meine prüfungssammlung nicht, und hier um forum gibts nur die 09er angaben ^^ danke schonmal
Hier die Angabe
Hier ist Bsp 4 von 2011.
Ich bin mir aber nicht sicher, ob das so passt…
Auf die letzte Konstante komme ich irgendwie nicht. Weiß jemand vielleicht wie es weiter geht?
EDIT:
Ich hab gerade bemerkt, dass sich auf der zweiten Seite in kleiner Schreibfehler eingeschlichen hat:
es gehört natürlich
e_y^i=\frac{e_r^i\cdot sin(n\phi)+e_\phi^i\cdot cos(n\phi)}{sin^2(n\phi)+cos^2(n\phi))}
Bsp 4 2011.pdf (510 KB)
Danke für die Formelsammlung 
Mir ist nur aufgefallen, dass beim Biot-Savart Ausdruck in der Formelsammlung das ³ unter dem Bruchstrich fehlt. Nicht das da irgendwelche blöden Fehler passieren…
was is der eindeutigkeitssatz?
Eindeutigkeitssatz des elektrischen Potentials:
V_1, V_2\text{ … Loesungen von } \partial^2 V=0
\
\
\Delta V=\partial_m\partial_m V
\
\
0=-\int_G \mathrm(V_1-V_2);\partial^2 (V_1-V_2),\mathrm{d^3}x=
-\int_G \mathrm;\partial_i,\left[(V_1-V_2) ;\partial_i,(V_1-V_2),\right],\mathrm{d^3}x+
\int_G \mathrm;\partial_i,\left[(V_1+V_2) ;\partial_i,(V_1-V_2),\right],\mathrm{d^3}x
Das = folgt aus der Inversen Produktregen. Wir wissen außerdem, dass der letzte Term größer Null sein muss.
-\int_{\partial G} \mathrm(V_1-V_2);\partial_i ,(V_1-V_2),\mathrm{d^2}f^i+
\int_G \mathrm;\partial_i,(V_1-V_2);\partial_i ,(V_1-V_2),\mathrm{d^3}x
Daraus folgt, da die Potentialdifferenz am Rand, und damit der erste Term, 0 sein muss:
\partial_i, (V_1-V_2)=0 \text{ und } V_1-V_2=const.
\
\
\
\qed
Hat jemand das Beispiel einer dielektrischen Kugel im homogenen E-Feld gerechnet?
Es wäre ur toll wenn das jemand online stellen könnte!
Wo ist denn die Angabe zu dem?
Dazu gibt es keine Angabe
In der Fragestunde heute wurde dieses Beispiel in Analogie zu Bsp 4 2011 angesprochen.
Der Aufbau ist der selbe, nur mit einer Dielektrischen Kugel anstatt des Zylinders.
Hier mal meine Version zur dielektrischen Kugel! Hab alle anderen Angaben vom Zylinder Beispiel übernommen nur das Feld hab ich in z-Richtung gelegt!
War noch was wichtiges in der Fragestunde hatte heute leider keine Zeit?!
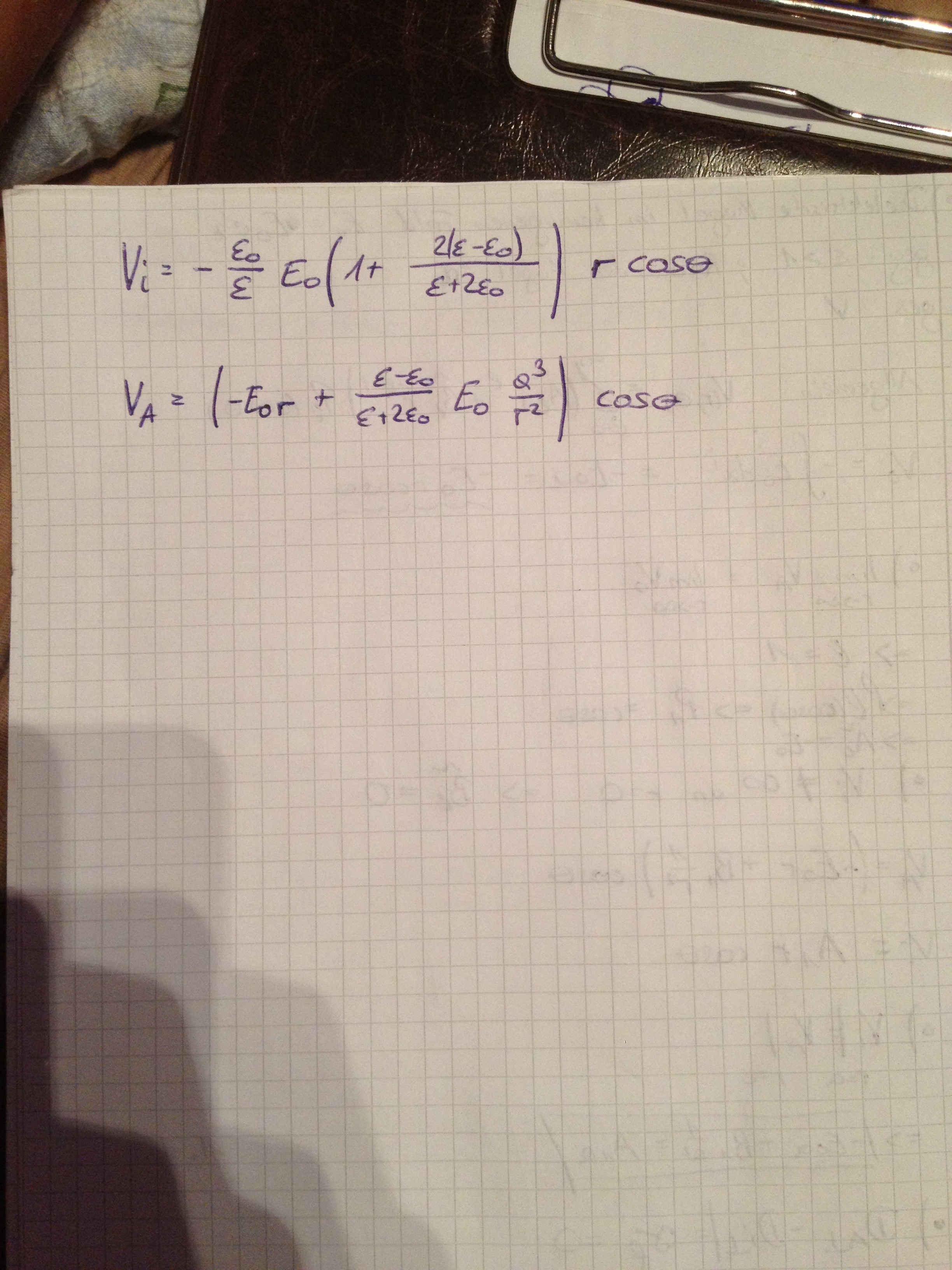
Die geladene isolierte Kugel mit Punktladung darüber (Spiegelladung) wurde gerechnet bzw. zumindest die Rechnung skizziert. Mehr ist sich dann nicht mehr ausgegangen. Irgendetwas mit allgemeiner Lsg. der Laplaceglg. ist sehr wahrscheinlich (außer unsere liebe Übungsleiterin wollte uns nur verwirren, kann natürlich auch sein).
Danke fürs durchrechnen!
Wieso gilt l=1 überall? Fürs V_außen versteh ich es, aber wieso gilt das automatisch auch fürs V_innen?
Was ich mir noch vorstellen könnte als Bsp wäre eine Metallkugel im konstanten äußeren Feld (haben wir in der Vo mal gemacht)…
Innen folgt aus der stetigkeits Bedingung von V! Außen ist l=1 und durch einen Koeffizientenvergleich muss es dann auch innen so sein.
Sehe ich das richtig dass es jetzt im Grunde 3 Varianten gibt?
Und zwar 1.) Äußeres Feld gegeben: Vorgangsweise wie in Max_Gains Rechnung
2.) Flächenladungsdichte gegeben: Vorgangsweise wie in der Übung wo wir die Sprungbedingung des E Felds an r=R verwenden und die Koeffizienten c_n berechnen durch Ausnutzen der Orthogonalität der Legendre Polynome (bzw. bei Zylinderkoordinaten Ausnutzen der Orthogonalität des sinus und cosinus.)
3.) Potential am Rand gegeben: Vorgangsweise wie bei 2.) nur dass man direkt durch die Stetigkeit des Potentials an r=R die Orthogonalität Nutzen kann
Ich hab das Beispiel 4 von 2011 nämlich auch auf die Art gemacht wie in der Übung, hat nur ETWAS länger gedauert…
hallo könnte vielleicht jemand der heute in der fragestunde war, seine mitschrift hochladen oder kurz schreiben was gemacht worden ist, welche beispiele gerechnet worden sind und ob sonst was wichtiges gesagt worden ist? wäre sehr hilfreich, danke!
Also es wurde eine Dielektrische Kugel im äußeren Feld gerechnet, eine Spiegelladungsmethode und ein Bsp zum Biot- Savart Gesetz gerechnet! Und dann wurde noch ein Kondensator Beispiel skizziert, welches so wie Bsp 27 aus den Übungen war, jedoch waren die Dielektrika nicht vertikal sonder horizontal getrennt.
Und noch eine Anmerkung zu Kugel oder Zylinder im äußeren Feld:
Das man l oder n = 1 setzen kann gilt nur für das äußere Potential und da auch nur für den Term der mit r anwächst! Also bei der Kugel gilt: \V_{A}=\sum_{l}(A_{l}r^l+B_{l}r^{-l-1})P_{l}(\cos\theta) wird über den Koeefizienten Vergleich zu \V_{A}=-E_{0}r\cos\theta+\sum_{l}B_{l}r^{-l-1}P_{l}(cos\theta)
Für das Potential im Innenraum gilt:
\V_{i}=\sum_{l}A’{l}r^{l}P{l}(cos\theta)
Über die Stetigkeitsbedingung an a folgt dann:
\-E_{0}a\cos\theta=\sum_{l}[A’{l}a^{l}P{l}-B_{l}a^{-l-1}]P_{l}(cos\theta)
Und daraus folgt nun das die Summe für alle Therme außer für l=1 verschwinden muss!