Lasset die Spiele beginnen…
tutorium2.pdf (42.9 KB)
Bsp 4.
MFG
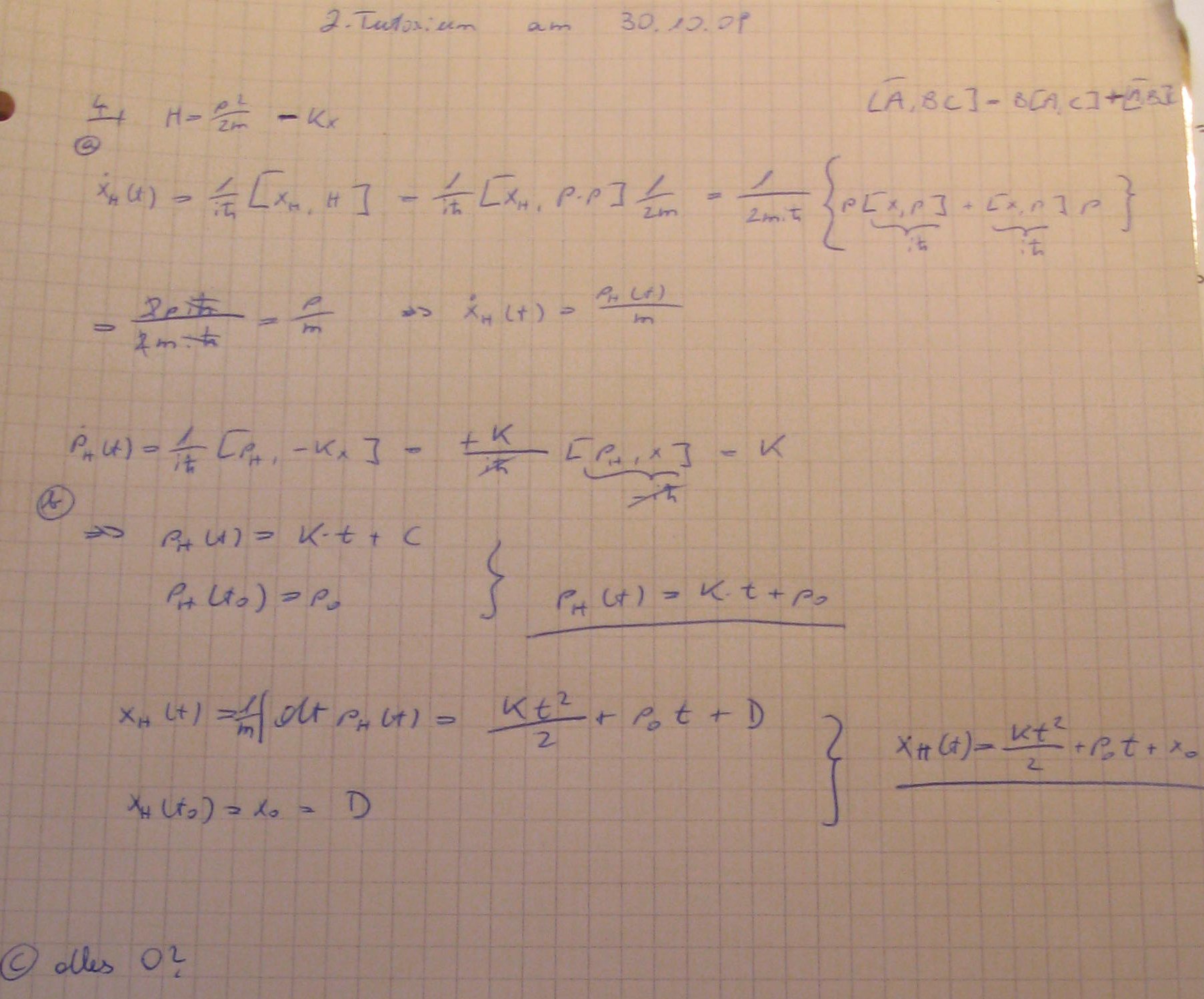
Hey,
Ad 1) Noch nix ![]()
Ad 2) Beim a hab ich den Dichteoperator umgeschrieben in Vektornotation mit Phasenfaktor 0. Dann den Zeitentwicklungsoperator augestellt und aus cos(…)+isigma sin(…) umgeschrieben durch Taylor und den Zustand entwickelt und auf einen Eigenvektor vom Sz projeziert.
Beim b das gleiche.
Ad 3)
Dichteoperator durch CG-Koeffizienten in die m-m Basis gebracht, und =Spur(Roh*A)
Ad 4) wollte ich zerst auch so ansetzen. Aber da gehen irgendwie die Operatoreigenschaften verloren für x und p, insbesondere der Kommutator [x,p] is null - was nicht sein. Das macht noch überhaupt keinen Sinn finde ich.
Hier mal die Beispiele 2 bis 4, ohne Anspruch auf Richtigkeit.(bin noch nicht dazu gekommen das alles nochmal durch zu lesen) Ich wäre sehr dankbar, wenn ihr mir eine kleine Rückmeldung geben könnt was ihr davon haltet, bzw. ob ihr bessere Lösungswege kennt.
Speziell der Lösungsweg von Bsp 3 scheint mir etwas schwindlich zu sein. Bsp 4 Ist sehr ähnlich wie der Post von Mario. Zu Bsp 2 brauch ich noch eine physikalische Interpretation
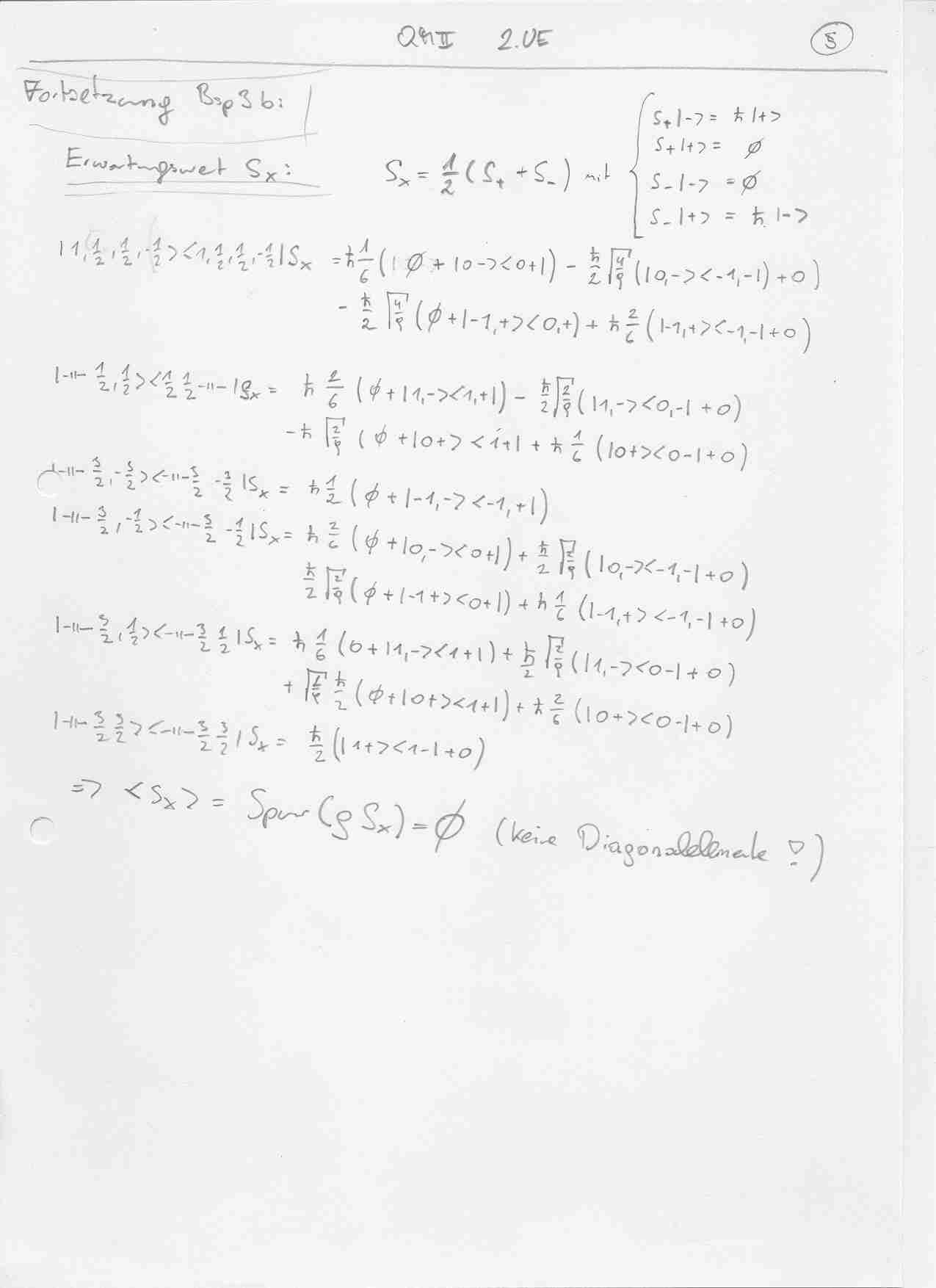
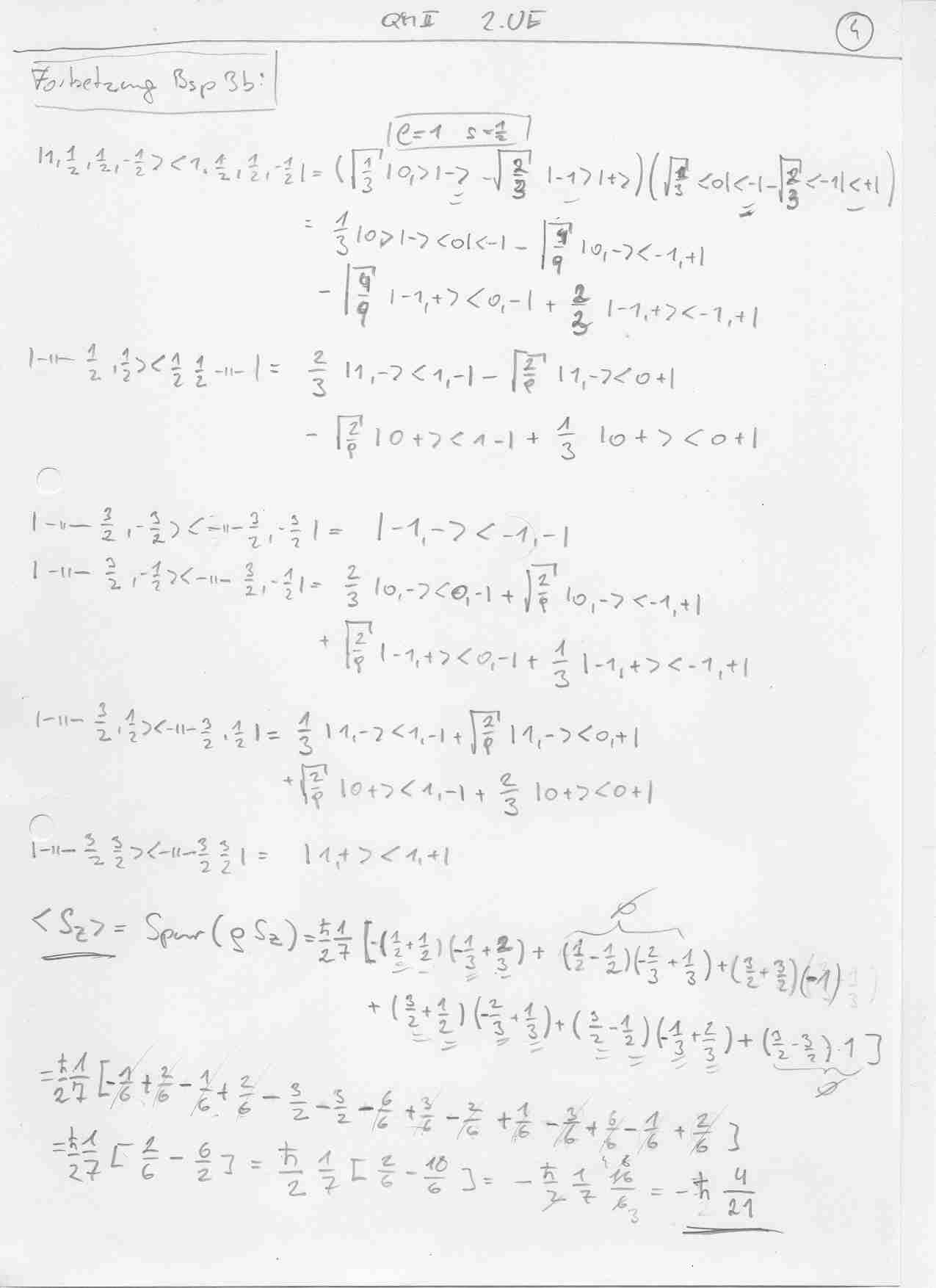
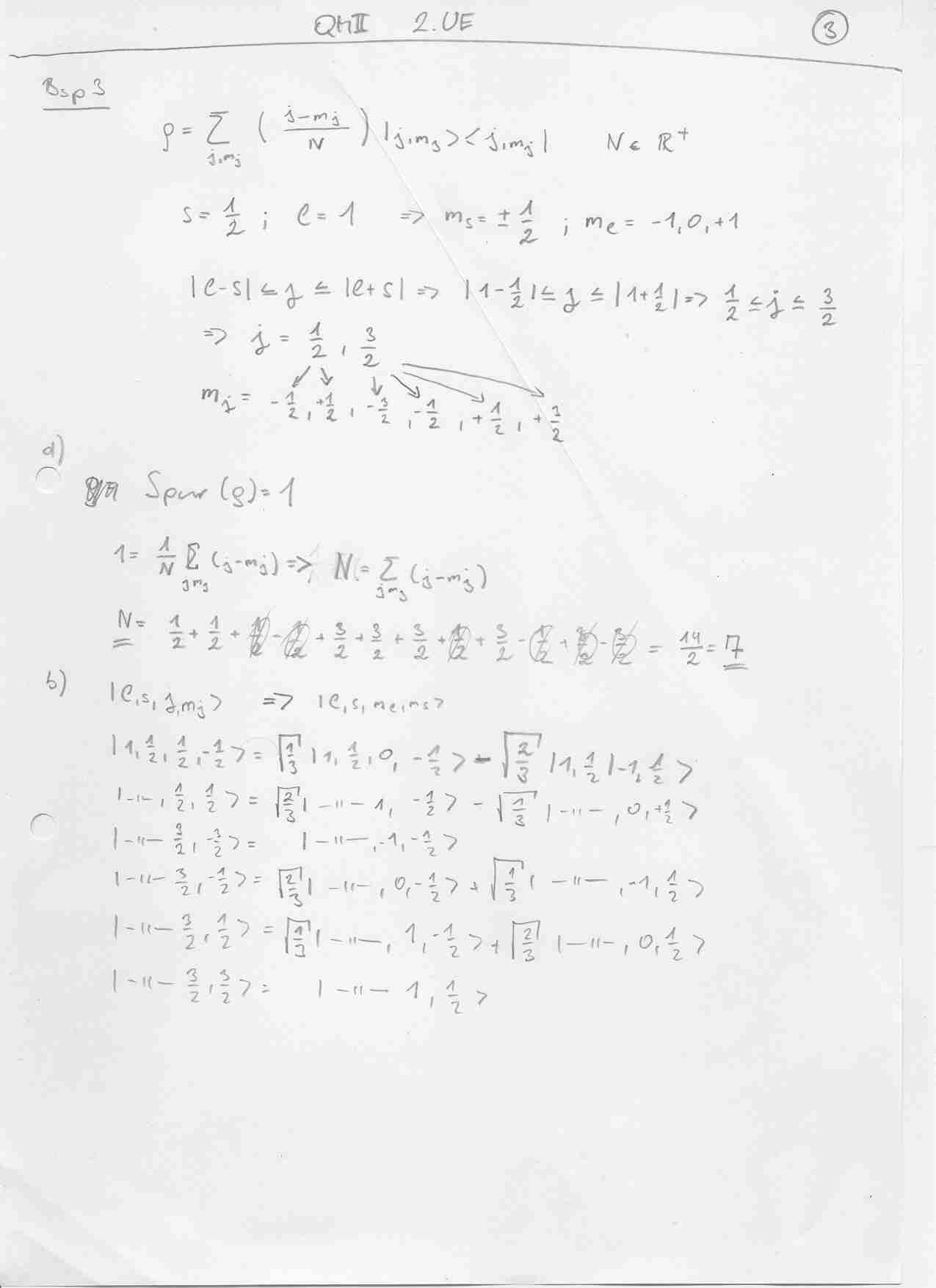


…und noch die Fehlenden letzten beiden Zettel…


Für alle die im Höhrsaal drei sitzen:
Der Tutor darf einzelne Beispiele von allen absammeln!
Ich soll das den Leuten aus dieser Gruppe sagen.
Was heißt das im -klartext - Jeder muss seine beispiele im Tut abgeben oder wie?
zum 1:
= 1/2 kbT weiters V(x) = 1/2Kx^2 = \mu/2w^2x^2 woraus sich w = \sqrt{k/\mu} ergibt
auf dem Angabezettel, der titiert wird, steht dann K=1860 N/m
dann noch E = \hbar*w * (n + 1/2)
und schon sollte es kein Problem mehr sein, zu n zu kommen.
Problem: es kommt a Sch… raus. (n+1/2 = 0.05)
weiß nicht, wo der Fehler ist.
Danke muhadib für das sehr schnelle Hochladen deiner Beispiele. Leider weiß nicht nicht, wie man es sonst rechnen könnte. Ein schönerer Weg beim 3. als die Superposition aller Zustände fällt mir auch ned ein. Allerdings glaub ich, du hast dich beim Erwartungswert für Sz verrechnet. sind bei mir -h*3/14
auch bitte ich, meine nicht vorhandenen Latex-Künste zu entschuldigen
edit: Unser Tutor hat gesagt, man sollte eine Reinschrift anfertigen, da es sein kann, dass Beispiele (aus Zeitmangel) abgesammelt werden. Zählt dann soviel wie eine Tafelleistung (0, 0.5 oder 1)
Also hier einmal mein Vorschlag für das Beispiel 1, beim Erwartungswert für n kommt zwar ein seltsames Ergebnis raus, die Rechnung „stimmt“ aber, glaube ich ![]()
Für Rückmeldungen wäre ich sehr dankbar.
Muhadib beim dritten Beispiel krieg ich auch <S_z>=-\hbar \frac{3}{14} heraus, du hast dich in beim Übergang von der vorletzten zur letzten Zeile verrechnet. Ich würd auch keine bessere Methode für das 3. Bsp. wissen, sonst hab ich zumindest die gleichen Ergebnisse.

Ich habe das erste Beispiel genauso. Meine Werte sind minimal anders - liegt aber an meinen Rundungsfehlern. Kann mir b) ebenso wenig erklären!! Da ich es unabhängig von dir gerechnet habe wirds aber im großen und ganzen schon passen - denk ich mir zumindest.
Bei 3b) bekomme ich für den Erwartungswert in z-Richtung 0 heraus - sehr strange ![]()
Danke für euren Hinweis auf den Rechenfehler in meinen Beispielen. Ich werd das mal korregieren
Für das erste Beispiel empfehle ich einen kurzen Review des Bsp. 24 aus Statististischer Physik I im SS08 ![]()
Könnte bitte jemand Bsp. 2 und 3 online stellen?
Vielen Dank!