Hier mal die Angabe
und hat schon vielleicht wer was zu 3.1g)
tutorium3_angabe_m(1).pdf (44.6 KB)
alles bis auf 1g)
bei 2b) wär ich über eine andere lösung dankbar weiß nämlich nicht ob das so stimmt
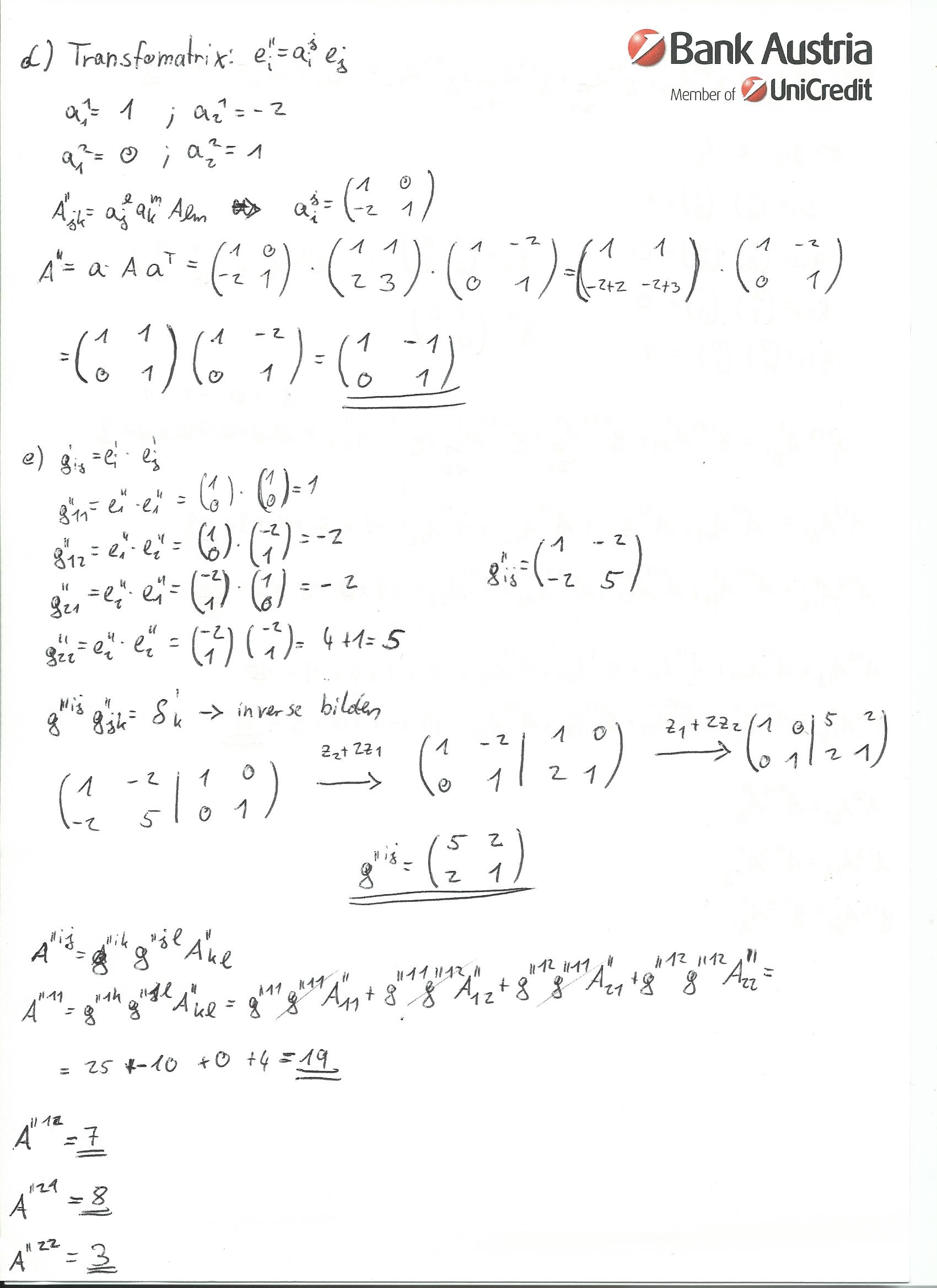
Bezüglich deinem Beispiel 1d) schaut gut aus, aber wieso kann man annehmen, dass A’'=a \cdot A \cdot a^T wenn bei dieser nicht orthogonalen Basis a^T \neq a^{-1} ist?
du hast recht sollte eigentlich ja nicht so funktionieren. aber ich muss sagen ich hab mir darüber eigentlich keine gedanken gemacht, wollte einfach nicht so viel schreiben wie bei a und hab dann einfach die matrixform genommen 
aber es kommt doch das gleiche raus wie wenn man es ohne matrix macht oder?
Servus sumpe,
Ich habe eine Frage, bist du dir sicher wegen deinem 3b? Dem letzten Umformungsschritt von delta jdelta jvi?
Weil im Endeffekt hast du einen Vektor minus nen skalar dastehen, das kann doch nicht ganz stimmen?! außerdem müsste bei einem ‚freien‘ Index (dem i) ein Vektor rauskommen…
Und der Laplace gäbe dir einen Skalar…
Ich muss ehrlich gestehen dass wir nicht wissen (bis jetzt wie man das anders machen könnte… aber vllt fällt dir was ein?
lg
rough
Edit: Du hast recht… lob an Google… aber warum stimmt das? Vektor minus skalar?!
du darfst nicht vergessen das v ein vektor ist und kein skalar
http://www.ipf.uni-stuttgart.de/lehre/online-skript/mathe/d12.html
Hey, vielen Dank, sumpe.
Bei 2b) kann ich nicht nachvollziehen, was du mit dem Term |ε_ijk a_j b_k |² machst.
ich hab mir hab mir einfach mal das kreusprodukt a x b aufgeschrieben normiert und das dann quadreirt und dann in indexschreibweise geschrieben
bin mir aber nicht sicher ob mann das machen soll oder ob es da noch nen anderen weg gibt
hat irgendwer 1 g)?
1g) niemand ?
leider nein 