is ja noch ein bissl zeit aber ich fang halt schön langsam wieder mit der angabe an.
tutorium4.pdf (45.9 KB)
Hier die Beispiele eins und zwei
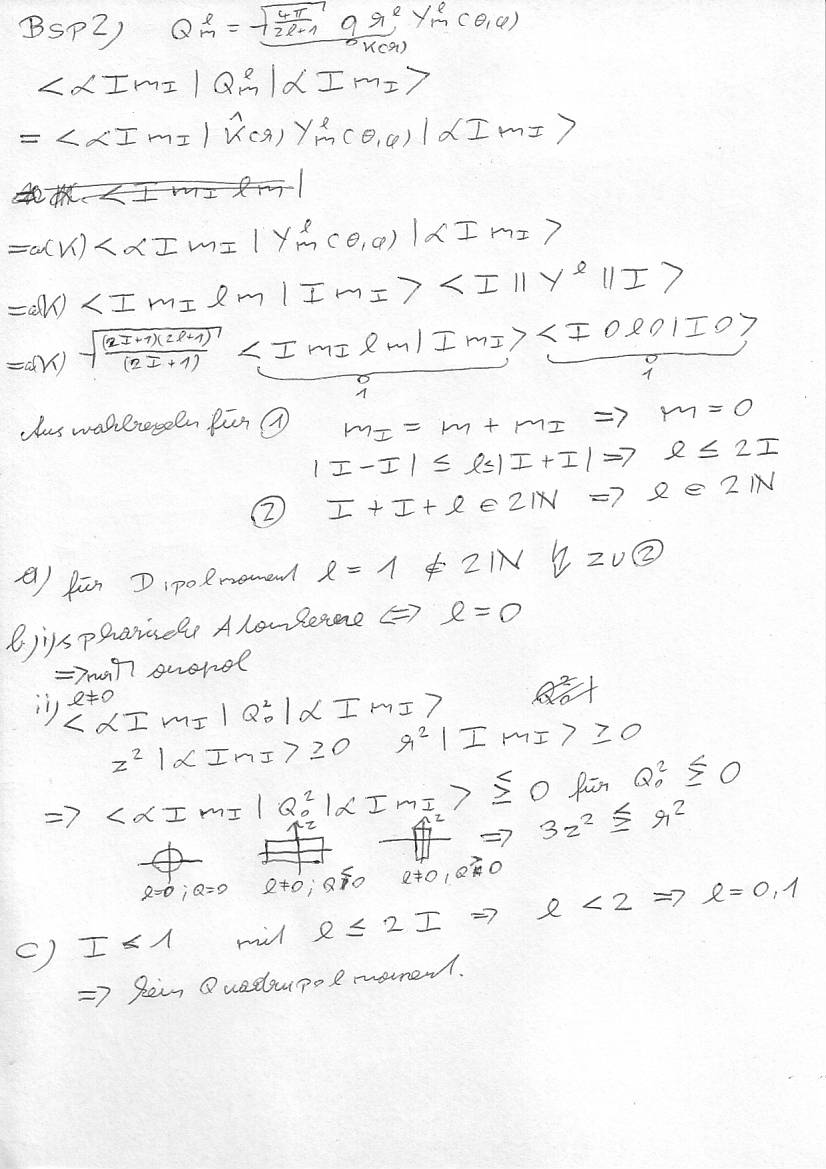

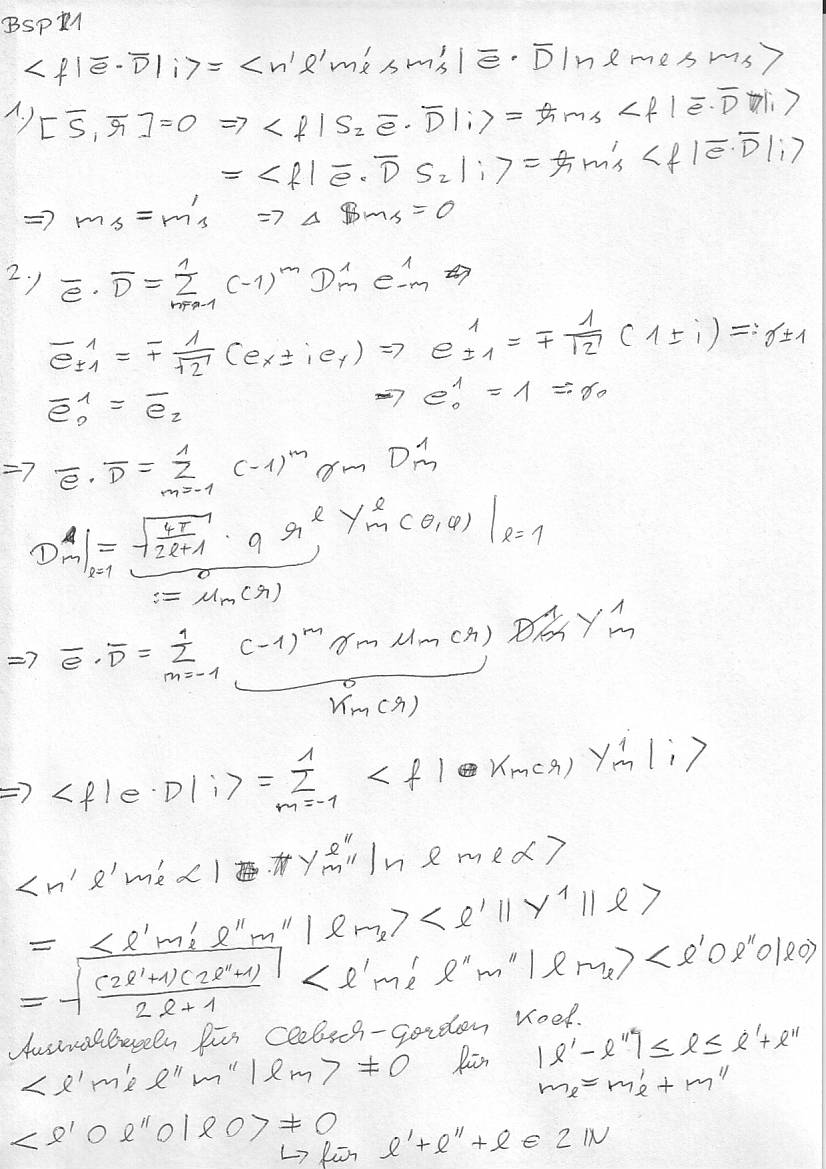
Und das Beispiel 3
P.S. Weiß man schon was Prüfungsstoff ist

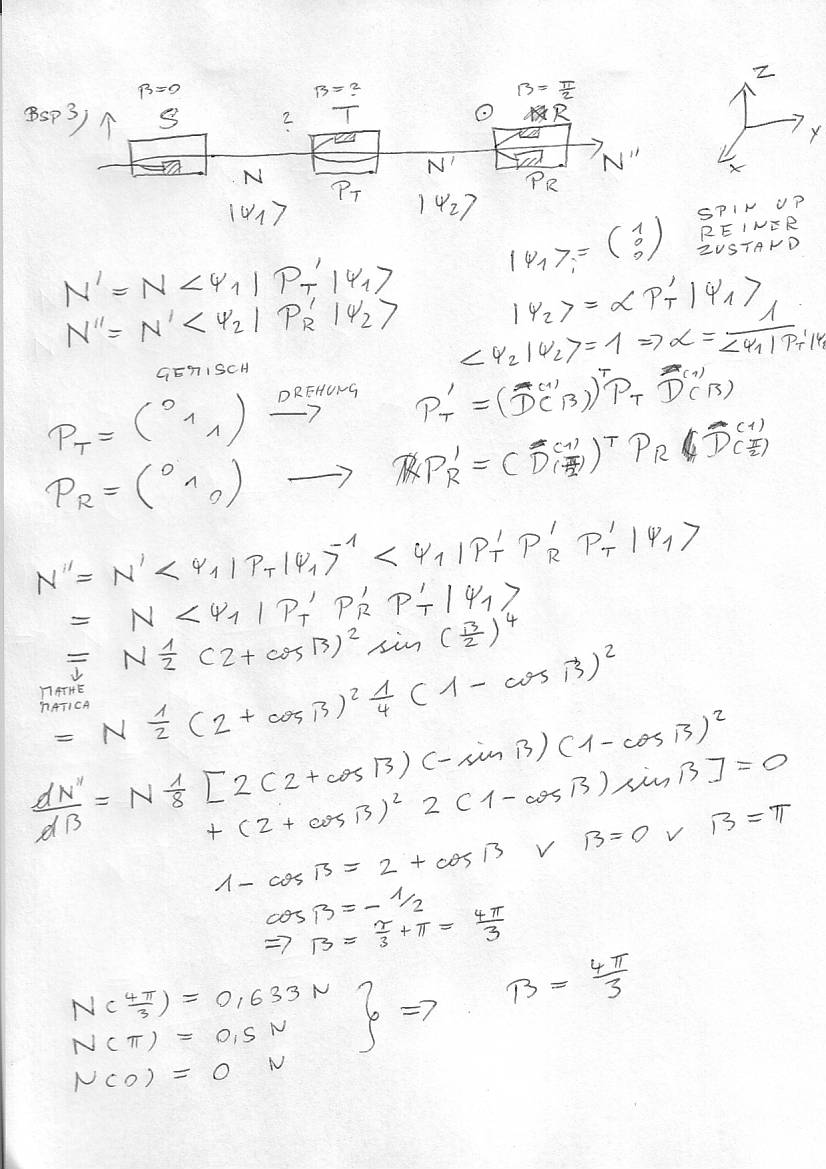
Hier noch Beispiel 4, bei c bin ich mir nicht sicher, ob die Rechnung stimmt, obwohl das Ergebnis logisch ist, da bei t=0 konstante Kraft -x Richtung auf das Teilchen einwirkt und somit der Erwartungswert auch nach links verschoben werden muss.
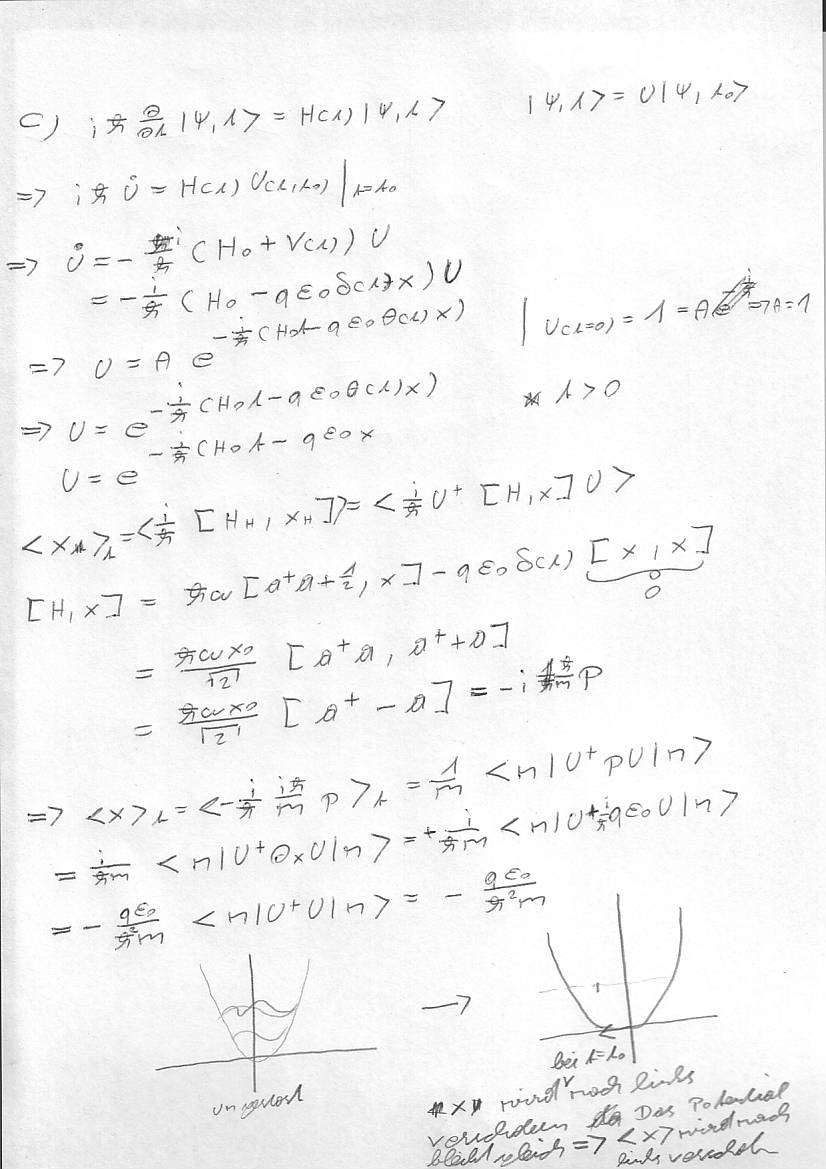

danke fürs onlinestellen!
woher kommt beim kommutator [H,x]=-ih/m*p das p beim ergebnis?
das p sehe ich schon ![]()
aber wo ist die zeitableitung vom erwartungswert hin? müsste es nicht sein d/dt* ?
Naja _t ist ja eine Observable und daher ist die Zeitentwicklung im Heisenbergbild durch den Kommutator \left[_H,H\right] gegeben und das <\left[x_H,H\right]>, der Beweis dazu ist im Cohen zu finden.
kannst aber auch leicht herausbekommen
\frac{d}{dt}=\frac{d}{dt}<\psi|x|\psi>=\frac{1}{i\hbar}<\psi|xH-Hx|\psi>+<\psi|\frac{\partial}{\partial t}x|\psi>
Wobei einfach
i\hbar \frac{d}{dt}|\psi>=H|\psi>
verwendet wurde
danke, jetzt verstehe ich es. ![]()
eine andere frage, bei bsp 3, seite 2, die lange multiplikation…
der projektor für R ist 0 ausser 1 in der mitte. die drehmatix ergibt aber für cos(pi/2)=0. dadurch wäre die multiplikation ja 0, oder?
ich verstehs noch nicht.
man berechnet sich da ja die änderung des erwartungswerts, ich will doch aber den wert wissen. müsste ich da am ende nicht noch integrieren?
Auch von meiner Seite nochmals Danke für‘s hochladen.
Eine Frage zu 3: Bei der Bestimmung der Normierungskonstanten \alpha multiplizierst du von links \langle \Psi_2 \mid, wie kommst du dann auf \langle \Psi_1 \mid P_T’ \mid \Psi_1 \rangle?
Die Normierungskonstante sollte mMn auch ^1/2 sein, so wie sie dasteht. Du hast trotzdem richtig weitergerechnet. Der Grau ist da sehr hilfreich übrigens!
Allerdings hab ich bei dem Beispiel3 auch das =0 Problem, da der Projektionsoperator des um Pi/2 gedrehten Apparates immer 0 wird.
Beim harmonischen Oszillator ist der Erwartungswert von x doch Null. Durch Einschalten des E-Feldes verschiebt sich dieser aber in Richtung des Feldes (bzw. dagegen, je nach Name der Ladung), also entspricht die Änderung hier auch dem neuen EW. Wüsste nicht was noch zu integrieren wäre.
Wo steht das denn, ich finde es nicht?!
ok anders ausgedrückt: es ist die ableitung, also die änderung mit der zeit, um die gesamte änderung zu bekommen muss ich über die zeit integrieren, denk ich mir zumindest.
Okay, jetzt sehe ich‘s auch und gebe dir völlig recht ![]()
EDIT: Eine zeitl. konstante Verschiebung ist auch irgendwie nicht so anschaulich.
Hey Danke fürs online stellen!!
Ich habe eine Frage zum ersten Beispiel:
Bei der Zerlegung des Polarisationsvektors e_{-m}^{1}=e_{\pm 1}^{1}=\mp \frac{1}{\sqrt2}(e_{x}\pm ie_y) folgerst du e_{\pm 1}^{1}=\mp \frac{1}{\sqrt2}(1\pm i)=\gamma_{\pm1}.
Das würde heißen e_{x}=e_{y}=1, oder? Kann man das so einfach annehmen? Oder verstehe ich was falsch?
Kenn mich leider mit den sphärischen Operatoren nicht gut aus, bin für jede Hilfe dankbar! ![]()
hat irgendjemand 4c und kanns erklärn?