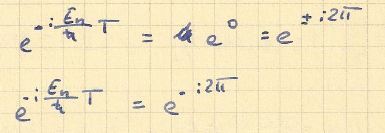Hier mal die Angabe:
tut5.pdf (139 KB)
Die Lösung des 2. Beispiels befindet sich in der Aufgabensammlung von Prof. Grau, Bsp. 1.24.
Aufgabensammlung Quantentheorie.PDF (4.31 MB)
zu 3a)
irgendwer C = ± wurzel(1/7L)
???
danke im voraus,
lg, stani
ja, das kommt mir auch raus für C
Hallo,
Beispiel 2:
q_ue5_bsp2.pdf (568 KB)
Vielleicht kann ja noch jemand Bsp. 1 und 3 beisteuern ![]()
mfg
hier eine inspiration für die 5.ue…
Tut5.zip (3.29 MB)
Hi!
Ein paar Fragen bezüglich der Lösung von Stefan13579 und insbesonders des 3. Beispiels:
Bin ja schon fast an a) gescheitert ohne der Winkelfunktionsidentität ![]()
1.: Wie kommt man da zum Schluss, dass die Mischterme 0 ergeben? Für x und y müsste man ja bei Mischtermen zwei ver. k´s einsetzen und erhält so durch Plus und Minus im Argument ver. Werte.
2.: Es ist doch bei b) überhaupt nicht notwendig psi^2 auszurechnen!? (-> Ausser man plottet dann die Aufenthaltswahrscheinlichkeitsdichte am PC)
3.: ad:d) Warum kann man die Wahrscheinlichkeit einen Energiewert zu messen einfach mit dem Betragsquadrat des entsprechenden Entwicklungskoeffizienten beschreiben?
Wahrscheinlich werden sich auf meine Fragen ein paar Kollegen auf den Kopf greifen ![]()
LG
Zu 1): wenn du die cos integrierst kommen sin raus. An der Stelle L eingesetzt sind das immer vielfache von Pi wo der sin bekanntlich 0 ist. An der Stelle 0 ist er sowieso immer 0.
Zu 2): das Psi^2 wird eben genau für den Plot ausgerechnet.
Zu 3): das haben wie in der VO gemacht: <a_i|A|a_i>=<a_i|a_i|a_i>=a_i<a_i|a_i>=a_i, wobei |a_i> eigenfunktionen und a_i eigenwerte von A sind.
In unserem Fall: <Psi|E|Psi>=[Sum(a_nPhi_ne^(iwt))]E[Sum(a_mPhi_me^(-iwt))]=;E nach rechts auf Phi_m wirken lassen ergibt ein E_mPhi_m;=Doppelsum(a_na_mE_mPhi_nPhi_m)=; Phi_n*Phi_m ist Delta_n_m;=Sum(|a_n|^2E_n)=Sum(p_nE_n)
Danke für die Antwort!
ad.1.:Habe ich mir heute eh noch mal überlegt und gleich überrissen;-) Die Frage war wieder mal ein Schnellschuss.
ad.2.:Das muss wohl in der Vo an mir vorbeigegangen sein.
Ciao
Nun ja… man benutzt die Eigenschaften der Box-Eigenfunktionen. Und zwar ist < Phi_i | Phi_j > = delta_i,j !! und dementsprechend sind alle mischterme beim integrieren über das gesamte intervall 0. bei den reinen termen kann man hingegen die konstanten faktoren herausheben und dann bleibt das integral über < Phi | Phi > übrig und das widerum ist 1. also erspart man sich komplett das integrieren.
Ja, eigentlich schon. allerdings ist es recht anschaulich, wenn man sich vor augen führt, wie die zeitabhängigkeit zustande kommt. und zwar immer nur durch die mischterme.
Die Wahrscheinlichkeit, dass ein gewisser Eigenzustand ein Teil deines Zustandes ist, ist durch die Entwicklungskoeffizienten gegeben. Dies Eigenzustände haben aber ganz charakteristische Energien. Wenn ein Eigenzustand also mit der Wahrscheinlichkeit „p“ auftritt, dann tritt die Energie dieses Eigenzustandes im Energiespektrum auch mit der Wahrscheinlichkeit „p“ auf.
Ich hoffe, dass das hilft. Hab übrigens als Erwartungswert für E das rausbekommen:
= (89/14) * E1
und meine Periodendauer von Punkt c.) ist : T = (4mL^2)/(pi*hquer)
Mit welchem Programm plotet man 3b)? Mit C? Sorry, mach zur Zeit nicht Datenverarbeitung…
mit mathematica am besten ![]()
beispiel 2.nb (193 KB)
Kann mir irgendwer 3c erklären? Bzw. die Schritte dich ich unten angefügt habe.