Anbei die Angabe.
Ein für das erste Beispiel hilfreicher Link (vor allem ab Seite 8 unten):
http://www.engr.ucsb.edu/~shell/che210a/lecturenotes/The_canonical_partition_function.pdf
lg
didi
6.tutorium.pdf (108 KB)
hier mal das dritte keine ahnung ob das so stimmt
Deine Ausdrücke enthalten alle eine Summe über N von 0 bis unendlich = 1+2+3+…+unendlich. Alle deine Ausdrücke divergieren. Ich glaube das wird nicht stimmen.
Du solltest den Ausdruck hinter der Summe auf x^N/N! umformen, die Summe ist dann e^x, ist auch angenehmer zum weiterrechnen
so noch mal das drittte hoffe das es diesmal stimmt
hat sonst noch wer irgend was?
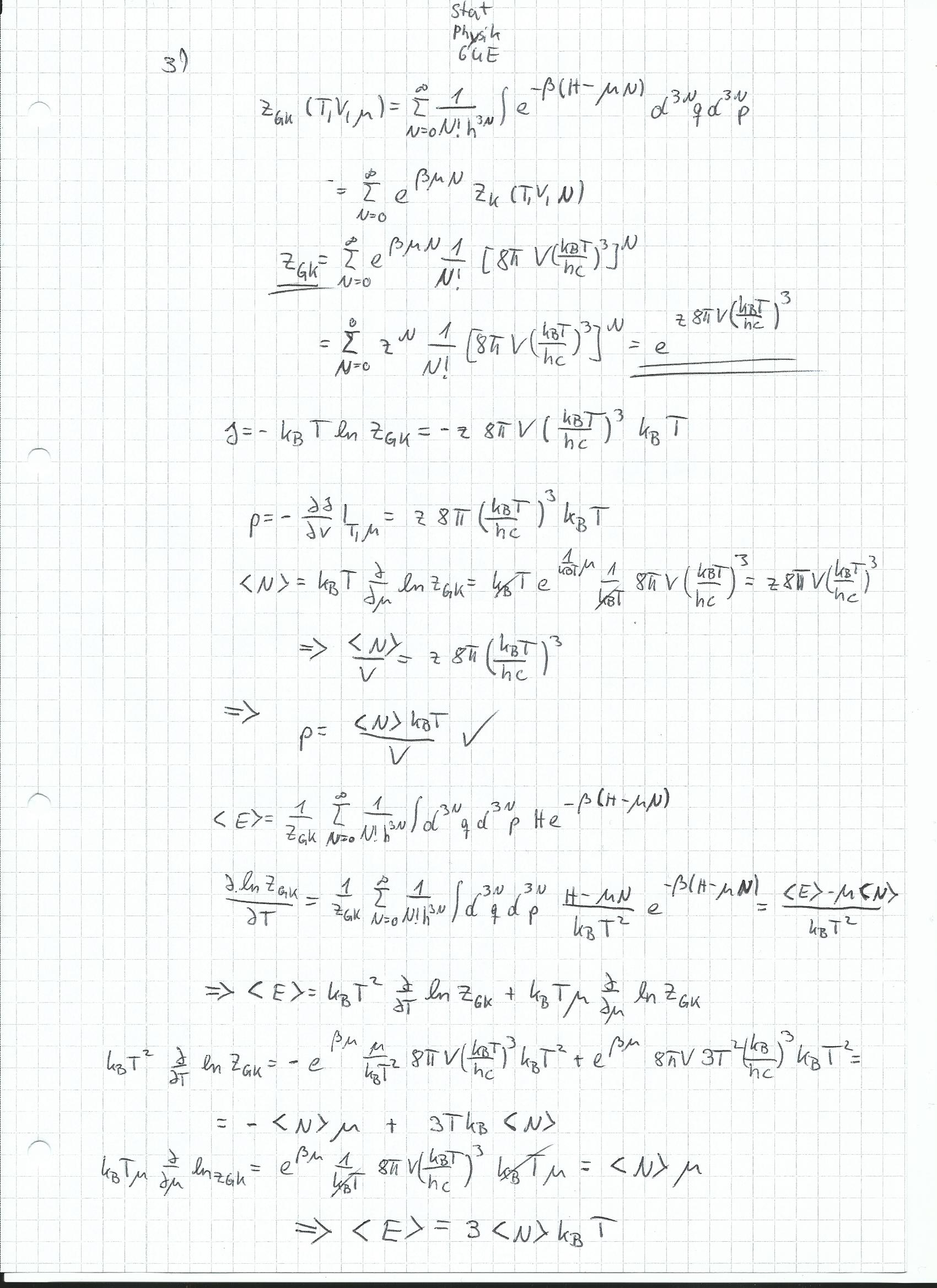
ich mach mir grad gedanken zu 1a)
da darfs eignetlich nur 1 möglichkeit(und ihre permutationen) geben wie man die Teilchen auf die zwei diskreten Energien aufteilen kann, wenn die Gesamtenergie und Teilchenanzahl vorgegeben sind. Seh ich das richtig?
Ja, das siehst du richtig. Die Gesamtenergie ist vorgegeben und daher gibt es nur die Möglichkeit, dass N1-Teilchen im Zustand 1 und N2-Teilchen im Zustand 2 sind. Also musst du nur noch die versch. Möglichkeiten abzählen, wie man N1 Teilchen aus N Teilchen herausnimmt → Binomialkoeffizient!
Lösungen sind auf WTF-Series Online:
http://www.wtf-series.com
hat wer 1c?
Mir scheint das Beispiel 4 von wtf Series entweder sehr fehlerhaft zu sein oder einfach schlampig geschrieben. Hat das jemand nachgerechnet?
Edit: Ich habe mich da wohl selber verrechnet. Komme auf das selbe Ergebnis!