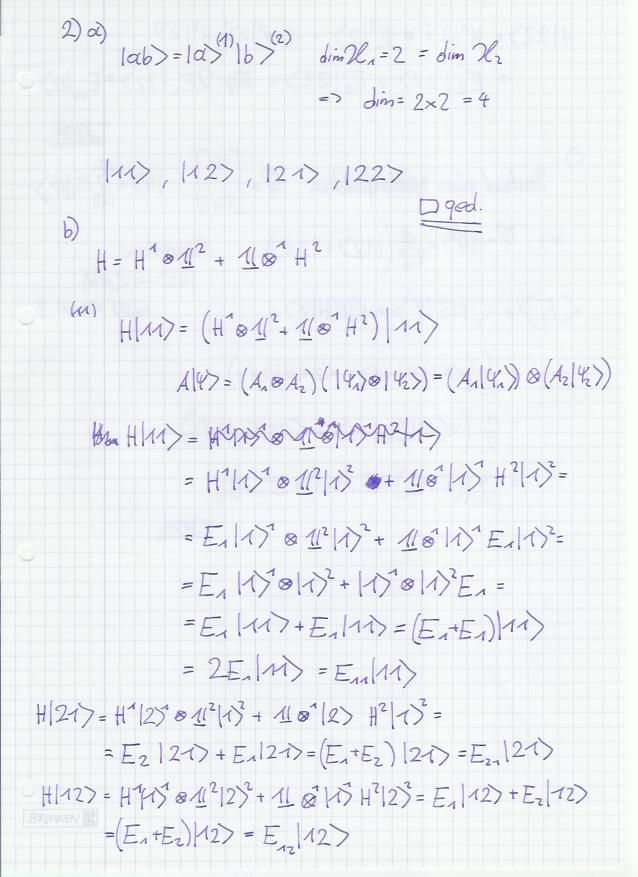
Danke mit der Formel für die getrennten Räume funktionierts bestens.
Fürs Archiv:
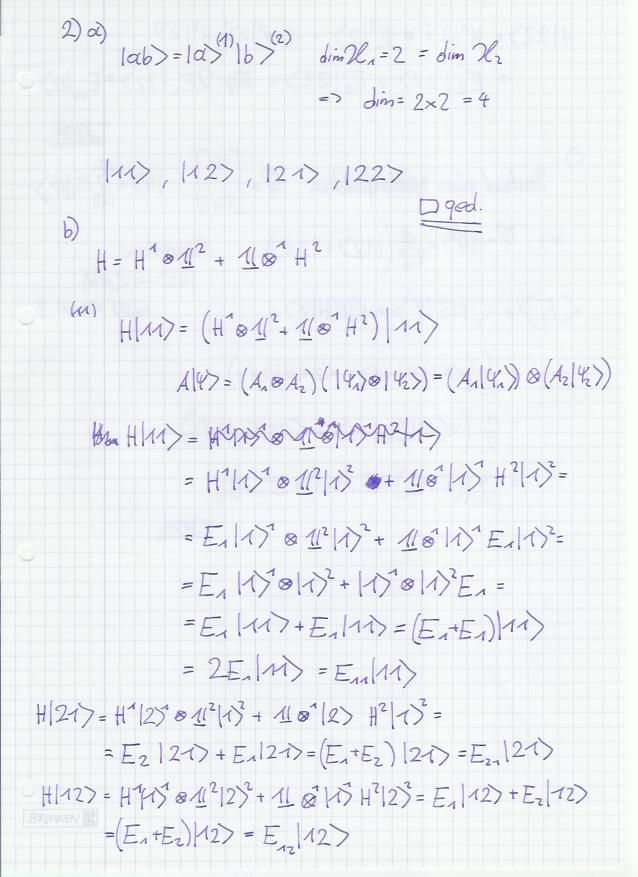
Die Begründung bei 1e fehlt allerdings noch.
ad 1e)
@Schlichtner: Noch ein Danke für Bsp 3.11 aus [Grau] =D>
Ich würde das jetzt so formulieren:
Der Definitionsbereich von H sind alle 2x-stetig auf dem Intervall (0,L) differenzierbaren Funktionen, die bei x=0 und x=L verschwinden,
d.h. D_H:=\left{ \ f(x)\ \in C^{\small 2}[0,L]|\ f(0)=f(L)=0 \right}
Diese Def.Bereich lässt sich auch physikalisch schön erklären, aber ich habe noch nicht ganz heraus, wieso genau man den Def.Bereich überhaupt einschränken muss, außer dass dann die „falschen“ Lsgs rausfallen 
für H^2 gilt für D_{H^2} nun:
H^2f(x) \Leftrightarrow H(Hf(x)) \Leftrightarrow Hg(x),\ g(x)=Hf(x), d.h. g(x) muss in D_H sein, g(x) ist aber genau -\frac{\hbar^2}{2m}f’‚(x)\ \Rightarrow\ f\in D_{H^2}\Leftrightarrow f\in C^4[0,L], f(0)=f‘‚(0)=f(L)=f‘'(L)=0.
Wie man aber für \psi(x)=\kappa x(L-x)\ \Rightarrow \psi’‚(x)=-2\kappa \Rightarrow \psi‘'(0)\ne 0 \Rightarrow \psi \notin D_{H^2} sieht, liegt es nicht im Def.bereich von H^2.
Edit: OK habs falsch verstanden. Versteh das auch noch nicht so richtig.
Noch etwas zum theoretischen Hintergrund bezüglich der Wahrscheinlichkeit bei 2de:
Es ist ja bekanntlich
\Psi =\sum c_{n}\Psi _{n}
Daher wird aus
<\Psi |P|\Psi >=\sum|c_{n}|^{2}<\Psi _{n}|P|\Psi _{n}>
jetzt besteht P aber aus
P=\sum |a_{k}><a_{k}|
Kann man da nun argumentieren dass unter der Summe k=n sein muss weil die Eigenfunktion „a“ nur zu einer bestimmten Wellenfunktion „Psi“ gehört?
Wenn man das nämlich macht ergibt sich schön die Beziehung:
<\Psi |P|\Psi >=\sum |c_{n}|^{2}\Psi ^{*}_{n}\Psi _{n}
und da die Wellenfunktionen Psi_n auf 1 normiert sind, ergäbe es einfach wieder die Summe aus den Wahrscheinlichkeiten, was wir hier ja berechnet haben.
ad 1.e)
Ich habe da eine seltsame Frage! Kanns sich da mal wer meine Rechnung anschaun, und mir erklären, wieso ich das anscheinend nicht machen darf! bzw. bin ich verplichtet, dass der Operator H^2 nur auf eine Seite wirkt? Weil ansonsten kommt mir das Ergebnis raus von oben!?
Danke
Bsp 1.e.pdf (251 KB)
Das ist ja das seltsame an dem ganzen Beispiel. (Ich verstehe auch nicht warum die 2ten Ableitungen dann auch die RB erfüllen müssen. Hab ne vermutung aber das klingt weit hergeholt)
Man kann im allgeinen nicht davon ausgehen dass Psi im Definitionsbereich von H bzw H^2 liegt (auch wenn es oft der Fall ist). In diesem Fall liegt Psi im Definitionsbereich von H aber nicht von H^2.
(Siehe Grau Seite 165, bzw pdf Seite 175) wodurch es sich nur durch dieses getrennte anwenden berechnen lässt.
Ich habe da noch eine Verständnisfrage: Ich berechne also den Erwartungswert dafür, einen Zustand aus dem Unterraum von P zu finden?! Und alle Zustände aus dem Raum haben nun die selbe Energie! Daher ist der Erwartungswert für den Zustand, gleich dem Erartungswert für die Energie?!
Ist das so Richtig?
Gehört evtl bei der Angabe vom 2. Bsp H:=H^{(1)} \otimes I_n^{(2)} + I_n^{(1)} \otimes H^{(2)}??
Wenn du die Hochzahl in der Klammer meinst, dass die nach der 1 steht und nicht nach dem Kreuz, dann denke ich schon. So hab ichs zumindest gerechnet.
Wegen 1e werde ich jetzt wohl einfach argumentieren dass der H Operator wegen dem Quadrat ja zweimal wirken muss, daher auch der Definitionsbereich für beide „Stammfunktionen“ gelten muss, weil der Bereich von H^2 wieder eine Teilmenge des Bereiches von H ist, und desshalb auch die 2ten Ableitungen die RB erfüllen müssten, was sie aber nicht tun.
Da Psi aber im Definitionsbereich von H liegt kann man das Quadrat ausrechnen indem man die Operatoren getrennt anwendet, wie bei einem Skalarprodukt mit sich selber.
Ne bessere Erklärung fällt mir nicht ein und ich finde auch nirgends was dazu.
Dieses Bsp habe ich auch noch hier gefunden, auf S.42.
Auf S.47 ist dann noch interessant „Physics of Self-Adjoint Extensions“.
Ist über die Selbstadjungierte Erweiterung von Operatoren, zeigt auch wie man diese konstruiert, blicke da aber nicht ganz durch 
hm danke. Viel hilft das bsp dort zwar auch nicht, aber zumindest bestätigt es die Definition was ich mir zusammen gereimt habe (siehe oben). Egal das muss fürs Tutorium mal reichen.