na dann mach ich mal nen kleinen anfang…
angabe und
2a) laut skript s. 159 gerechnet
komme auf 2,466 * 10^15 Hz → UV-strahlung
tut9.pdf (147 KB)
komme bei 2a auf das selbe…
was mich mehr interessieren würde, wäre 3c… 
hat da wer was?
ich komme nur auf einen Kegel mit 30° um Lz…
Lg, Kobold
servas,
dass ich auch mal was post und nicht immer nur mitschnorre 
a: 1/4 bzw. 25%
b: Erwartungswert = hquerWurzel(3)/4. Unschärfe=hquer/4.
c: Zustand schaut in die Richtung mit phi=90° und theta=45°, also (x,y,z)=1/Wurzel(2)(0,1,1)
kann natürlich auch ein kompletter schwachsinn sein, dann sorry für die falsche fährte!
@Kobold: ein Kegel kanns (denk ich mal) nicht sein, weil jeder Zustand genau EINER raumrichtung zugewiesen ist. hat zumindest der gute stefan in der VO gesagt…
lg, der nicht-so-gute stefan
meiner meinung nach ist die antwort zu 3c folgende:
man muss sich nur die zur definition der bloch-kugel gehörenden winkel ausrechnen, also theta und phi.
bloch-kugel: |x> = cos(theta/2) |+> + e^(i*phi)*sin(theta/2) |->
mein ergebnis: theta = pi/3 ; phi = pi/2
mit welcher idee seid ihr zu anderen ergebnissen gekommen?
Ich hätte gesagt, dass der Zustand in die Richtung phi=90 und theta=60 schaut.
Man muss doch bei der Berechnung der beiden Winkel lediglich in die Definition der Blochkugel einsetzen mit den Werten des Zustandes,oder?
das hab ich doch oben ^^ auch gesagt: und die werte sind dasselbe: theta = 60° = pi/3 und phi = 90° = pi/2 !!!
Tut mir Leid, dass ich dich einfach wiederholt habe, aber ich habe leider deinen Beitrag nicht gelesen gehabt.
Habt ihr schon eine Lösung für das 4. Beispiel mit dem B-Feld in z-Richtung?
Hab das 3c gerechnet wie das 1er Bsp. Ich glaube, dass sollten wir auch so machen. Es gib ja diesen Hinweis der auf das 1ste Beispiel verweist.
Es kommt mir das Gleiche heraus wie bei dem Ansatz mit dem Blochvektor. (phi=pi/2 , theta=pi/3)
Anbei …
P.S. Hab die Umformung der Winkelfunktionen nicht händisch durchgeführt, sondern Wolphram befragt.
QU1_Tutorium9_3c.pdf (95.2 KB)
falls einer so lieb wäre seine rechnerei zum dritten beispiel zu posten, wäre ich unendlich dankbar…
habe leider vor weihnachten ein paar VOs verpasst, und mit skriptum-selbststudium komme ich leider nicht wirklich weit.
weiters, hat jemand was sinnvolles zu 2b) ?
ich vermute mal dass der hinweiß darauf hindeutet, dass man da mit dem paritäsoperator zu zufriedenstellenden ergebnissen kommt… wie genau… null plan.
danke im voraus,
lg stani
Danke, Erik! Hab auch so gerechnet, nur nicht gewusst wie ich aus der Gleichung wurzel(3)sin_x*cos_y+cos_x=2 x und y bekommen soll!
jetzt passt es))
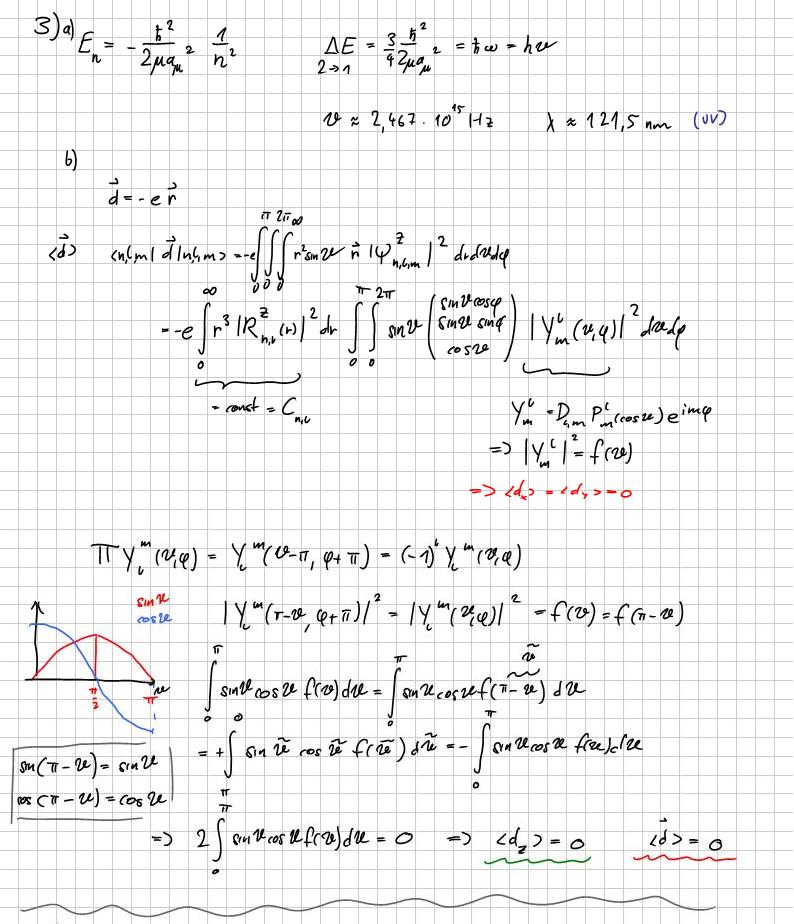
Also bei 2.b. schauts so aus.
mit P = P^-1 . P ist der Paritätsoperator.
<nlm|d|nlm> = <nlm|P P d P P|nlm> = <nlm|(-1)^L P d P (-1)^L|nlm> = <nlm|(-1)^L (-1) d (-1)^L|nlm> =
= -(-1)^2L <nlm|d|nlm> = - <nlm|d|nlm>
=> <nlm|d|nlm> = 0
da L eine gerade Zahl sein muss ist (-1)^2L immer 1 und daher <nlm|d|nlm> = - <nlm|d|nlm>.
LG
Erik
P.S. Tipp: Rechne beim 3er mit den Leiteroperatoren für S. Sx=1/2 (S+ + S-), Sy = 1/2i (S+ - S-) wobei S+|+> = 0, S+|-> = h(quer)|+>, S-|+> = h(quer)|-> und S-|-> = 0 .
hey leute, hat noch irgendjemand „umfangreichere“ lösungen anzubieten? hab mich noch nicht wirklich damit beschäftigt und jetzt drückt aber doch der schuh…
Ich wäre weiteren Lösungen auch sehr dankbar, komme einfach auf keinen grünen Zweig.
Und zu 3c.) wie löst man denn die Gleichung sqrt3*sin(theta)+cos(theta)=2, steh ich da einfach nur auf der Leitung oder gibts da einen Trick?
ich hab mir einfach die sin/cos -Werte zum gleichen Winkel angeschaut, die zur gleichung passen: sqrt3/2 für sinus und 1/2 für cosinus. Das ist dann Winkel pi/3
2tes beispiel. ist nicht von mir, habs in kopien von älteren übungen gefunden.angabe ist genau die gleiche gewesen.
Hey, hier sind meine Lösungen… das 2b stimmt aber nicht…
viel spaß damit
Scan_2199_001.pdf (1.27 MB)
Hat jemand die Skizze zu 3c.)? Wie schaut die bei euch aus?