wie kommt man von v=-A*\omega*sin(\phi) auf A^2 * cos^2 (\phi) + A^2 * sin^2 (\phi) = \frac{v^2}{\omega^2} ?
Weiß ich zwar nicht. Aber man kommt auf dasselbe ergebnis wenn man die formel 11.4c x(t)=C_{1}*cos(\omega_{0}*t)+C_{2}*sin(\omega_{0}*t) verwendet. Dann eben die Randbedingungen anwendet so dass man sich die C’s ausrechnet und dann die Formel A=\sqrt{C_{1}^{2}+C_{2}^{2}} verwendet. ![]()
Weiß jemand wie bei 4d die Gleichung gemeint ist wo Impuls und Kraft gleichgesetzt wird? Erscheint falsch. Auch in der Endgleichung für die Beschleunigung sind die Einheiten nicht korrekt. Aber:
Danke, Danke für’s Hochladen! Hast uns allen (mittlerweile 135 (!)) den Arsch gerettet ![]()
Edit: Okay, sorry. Is schon spät ![]()
Heyho habe hier mal die letzten drei Beispiele ausgearbeitet.
Ich weiß es ist sehr gekritzelt und wsh auch etwas fehlerbehaftet, deshalb bitte einfach fragen wenn was unklar ist, würd mich außerdem sehr freuen auf Fehler aufmerksam gemacht zu werden!
Habs letzte Übung leider etwas verpeilt ![]()
Lg Jakob
edit:
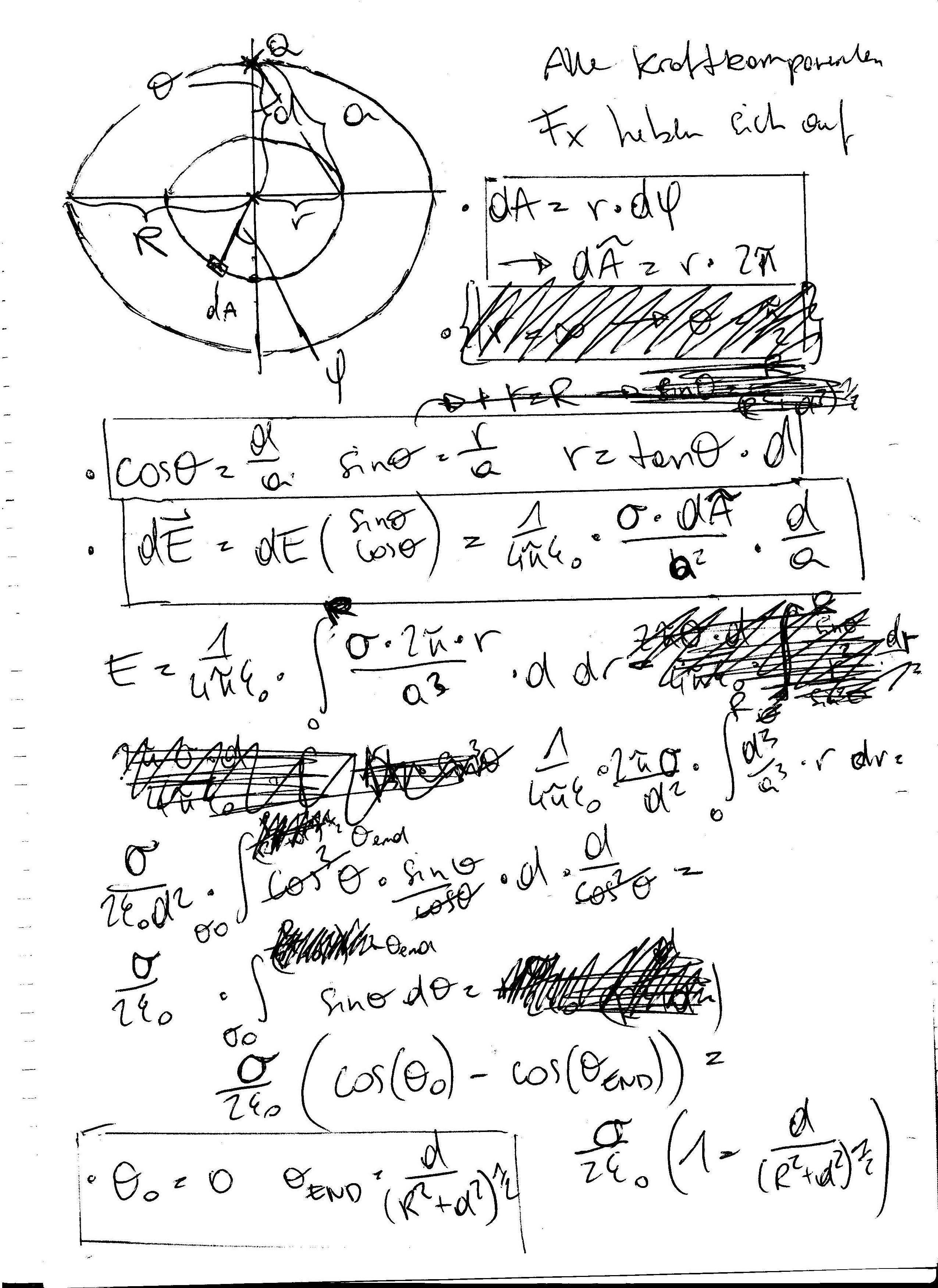
sorry, beim bsp 9 sollte stehen cos(\theta_{0})=1; cos(\theta_{end})=\frac{d}{sqrt(R^2+d^2)}, denn das sind die cosinus Werte wenn theta=0 und wenn r=R.
Und dà soll das ganze „Kreisring-Flächenelement“ sein, denn für dieses gilt dasselbe E-Feld.
Und um das Bsp vlt verständlicher zu machen, ich hab dasselbe gemacht wie in der VO, einfach die r und dr terme durch winkel terme und konstanten erstetzt und über den winkel integriert, aber diesmal nicht bis pi/2 sonder bis zum endwert \frac{d}{sqrt(R^2+d^2)}
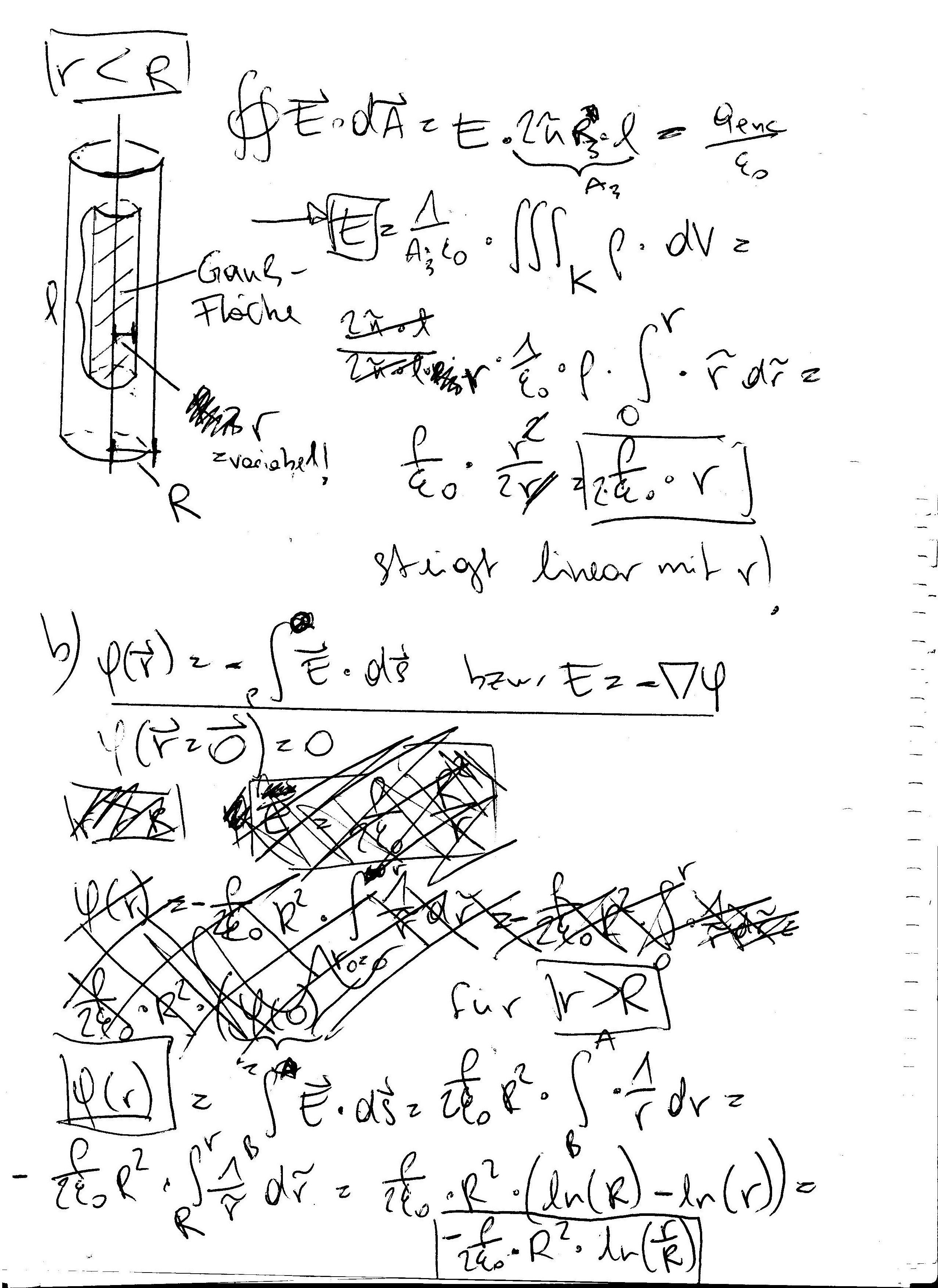
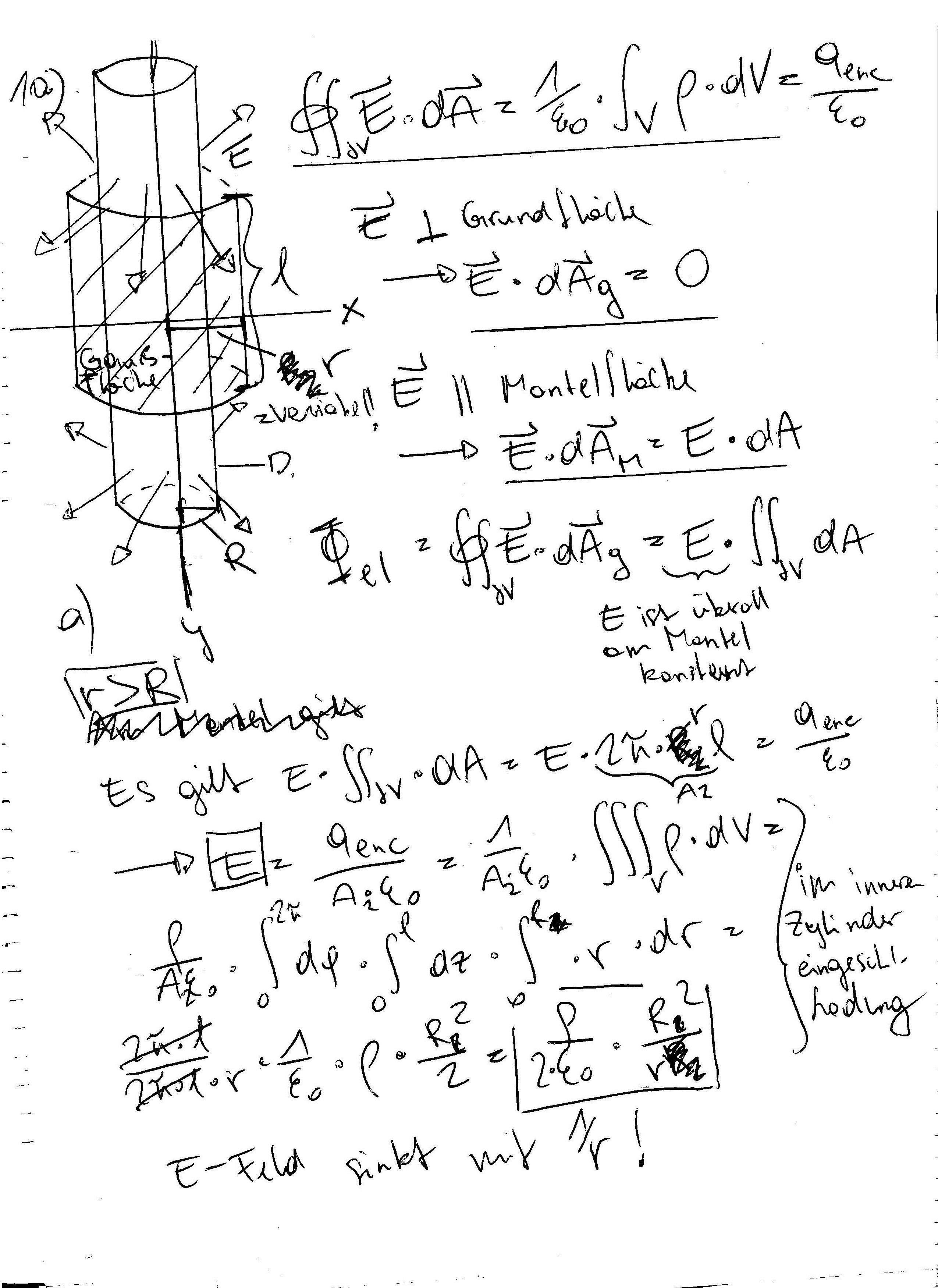
bei bsp 10, auf der 2. seite sollte in der 1. zeile klein r stehen R3 gibt es nicht ^^
R ist der Radius des normalen, gegebenen Zylinders und klein r steht für den Radius des äußeren/inneren Zylinders, dh den Ort an dem man sich befindet, dieser kann variieren.

und hier noch die Angabe
UE02 20130321 Angabe.pdf (691 KB)
also erstmal danke für die ausarbeitungen!
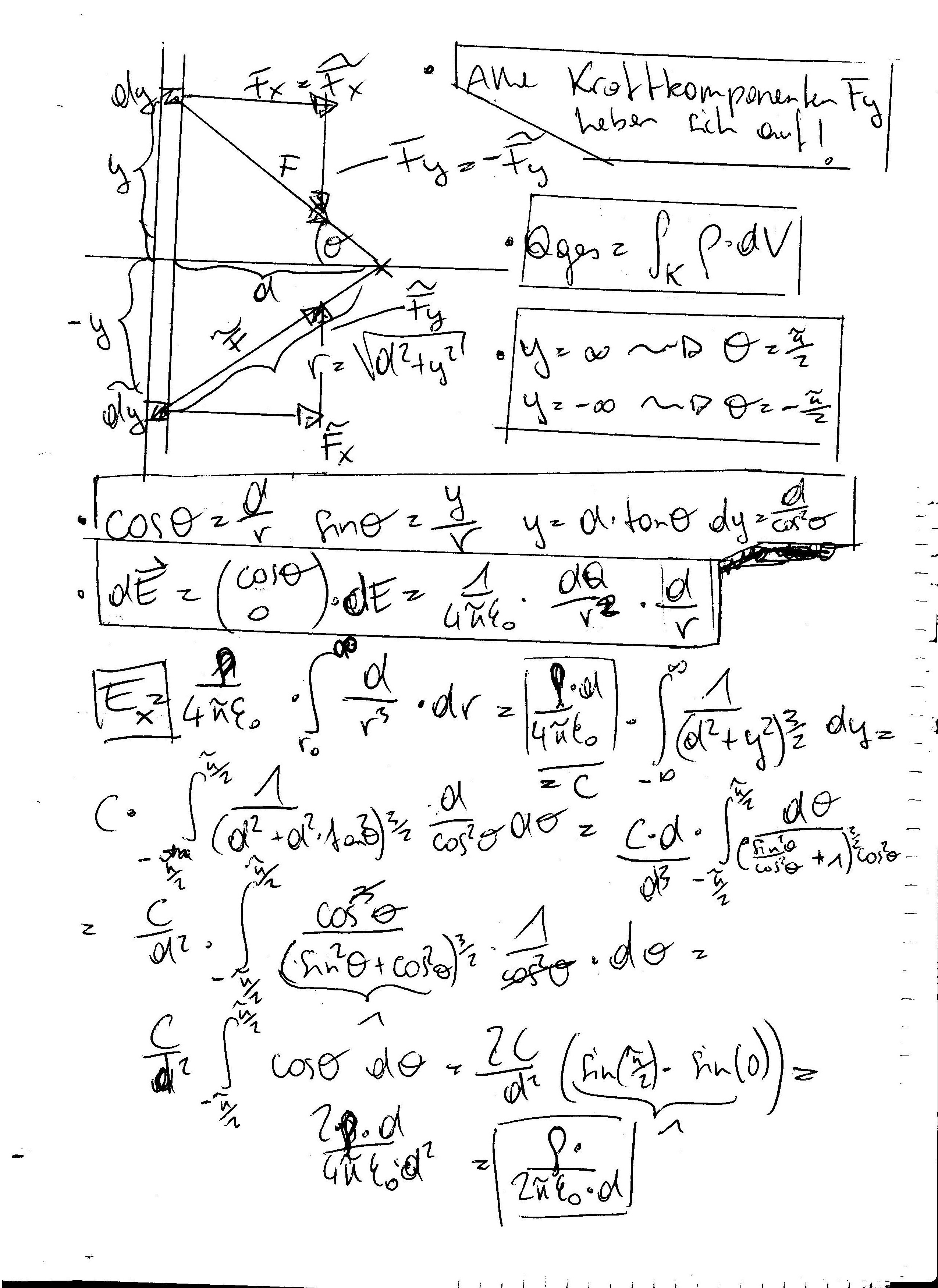
habs jetzt mal kurz durchgeschaut und hab eine frage zum 8ten beispiel. in der zweiten zeile in der E_x ausgerechnet wird ziehst du ganz rechts 1/d³ raus. wie kommst du da auf 1/d³, ich komm dort auf 1/d² und wenn ich das rausziehe kürzen sich alle d weg (weil ja bei deiner variable C ein d enthalten ist).
heyho, also aufs d^3 kommst du , da (d^2)^{\frac{3}{2}}=d^3
hier außerdem Bsp 6 (edit: Bsp 7) angehängt


äääh habe vorhin gesagt ich habe Bsp 6 angehängt, es Bsp 5 genannt, aber tatsächlich ist es Bsp 7 XDD
hier kommt jetzt das wirkliche Bsp 6:
edit: hab den fehler gefunden ^^
lg jakob

aja hab mein ^(3/2) verloren^^. danke.
ich glaube, du hast bei 6a) bei den Integralgrenzen einen Fehler, denn wenn du W1 null annimmst, setzt du ja quasi den Nullpunkt in Q1, daher müsste ja in den Grenzen der Betrag des Abstandes zwischen den Ladungen stehen, also bei Q1–>Q2 von unendlich bis 2a und bei Q1–>Q3 von unendlich bis sqrt(2)a. so hab mir ich das halt gedacht…
hmmm… aber ich habe mir hierzu folgendes gedacht:
Q2–>Q1 setz ich genau wie du gesagt den nullpunkt in Q1, und integriere bis -2a;
hier hab ich im Bsp einen Fehler, nämlich hab ich nur bis -a integriert (Danke ![]() )
)
Q3–>Q1&&Q2 setz ich den Nullpunkt in die Gerade zw. Q1, Q2 und hier heben sich die y komponenten auf, dh mich interessiert nur der x Abstand, also a
hier: nächster Fehler, im Bsp steht -2a XD
genau die Grenzen vertauscht…
Ich glaube aber noch weitere Fehler (vor allem in 6_3, stimmt iwas nicht ^^) drin zu haben…
hab mir daweil nur bsp 10 angeschaut, müsst ja das bsp 1.3.4.3 geladener stab im demtröder sein. lustigerweise is dein beispiel schlüssiger als des im trödler. was ich am trödler nicht versteh is, dass Q=(LamdaLpir^2)/(piR^2) is. wie kommt den der drauf?
danke im vorraus
hallo, also er kommt eig auf dasselbe wie ich, da er \lambda=\rhor^2\pi setzt, dh er ersetzt den Stab durch ne eindimensionale Ladungsanordnung mit einer Dichte wie der Stab…
das andere ergebnis im Potential erklärt sich durch die andere Normierungsbedingung
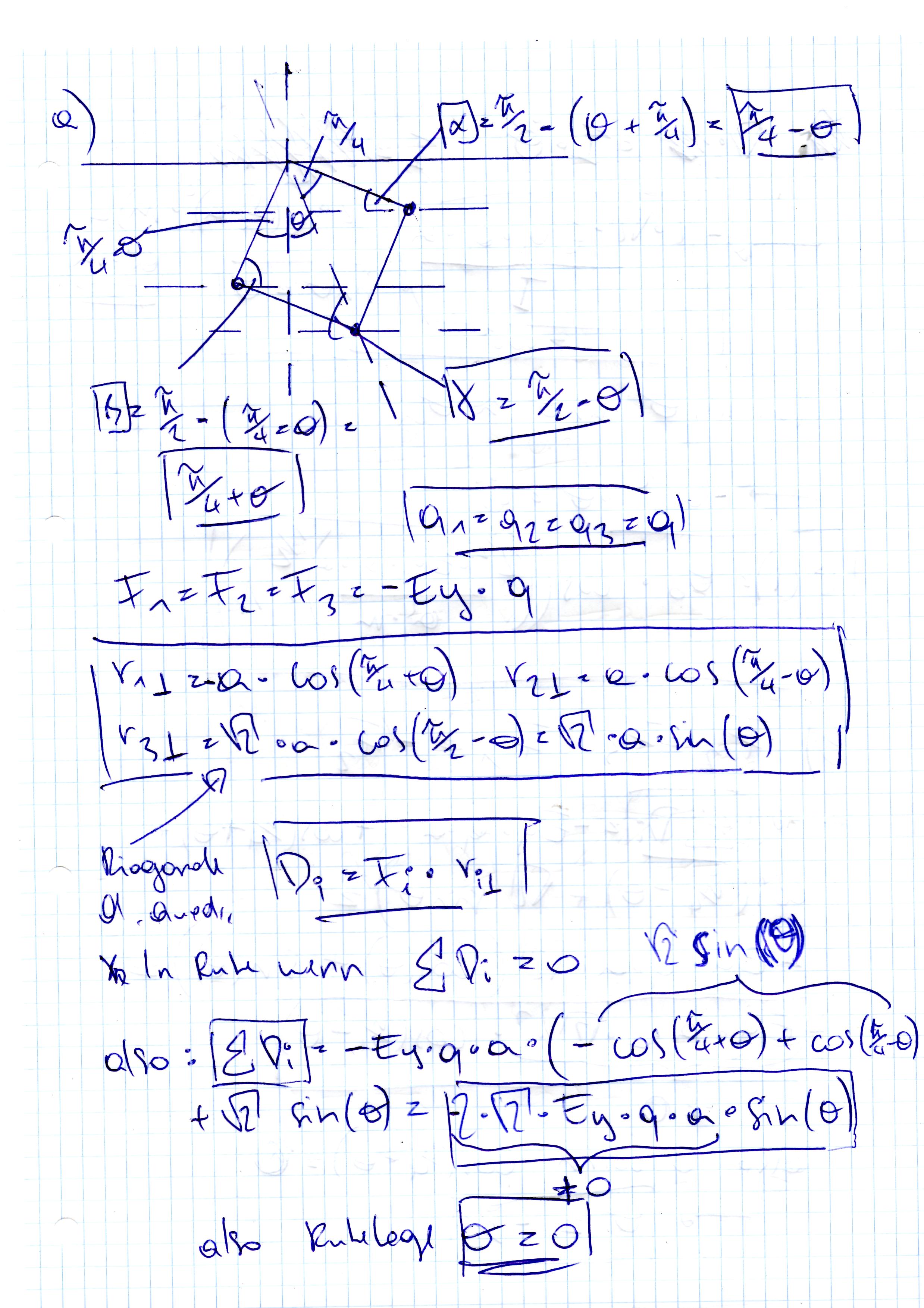
(edit:) Im Übrigen sollte bei Bsp 7 das Trägheitsmoment um die Drehachse
\sum_1^3 r_i^2m=a^2m+a^2m+(sqrt(2)a)^2m=4a^2*m sein
und bei Bsp 10 hab ich die Integrationsgrenzen bissl durcheinander gebracht, beim Potential für r<R sollte das Vorzeichen umgedreht werden… is positiv
Noch eine Frage an die Allgemeinheit:
soll ich die überarbeiteten Bsp 6a,d,e nochmal hochladen?
Sicher kein Schaden ^^
Danke
Eine Frage zu Bsp. 7:
Sollte man nicht auch das elektrische Feld berücksichtigen, das von den 3 Ladungen q1, q2 und q3 hervorgerufen wird?
ich weiß eh das des lamda = rhopiR^2 is, nur ich check net des Q, dass für r<R gilt ![]()


Hej zusammen,
hier mal meine Variante des Beispiel 6,
Weiß jemand von euch wie man bei Punkt d auf die Energie kommt, die frei werden sollte, wenn q4 an die Position x=0 gebracht wird?
Danke im Voraus!
Achtung: ich habe bei c das Vorzeichen vom Gradienten vergessen! Vorzeichen gehören somit bei c, wie auch bei e getauscht!
Bsp_6.pdf (746 KB)
@ is_eh_ois_trivial:
könntest du vielleicht bsp 21.9 aus deinem schlauen buch auch noch hochladen, damit man
nachvollziehen kann, wie man aufs dE vom ring mit radius r kommt.
das wär super.
oder hast das eh iwoher ausm internet?
Ich meine die Kräfte zw. den Ladungen werden durch die Stangenkraft kompensiert.
achso, naja ich stell mir das so vor:
im Innenraum wählen wir einen Zylinder mit Radius r, und die eingeschlossene Ladung ist Q=\int_K \rhodV bzw Q=\int_K \lambdadr nun ist die Dichte konstant, also ist es einfach DichteIntegral über den Körper
V=r^2\piL und damit Q=r^2\piL\rho=\frac{r^2*\piL\lambda}{R^2*\pi}
Im Äußeren wird offensichtlich der Stab als unendlich lange Anordnung von Punktladungen gesehen und damit ist der Körper einfach nur noch L und die Ladung Q=\lambda*L
Ich find allerdings diese ganze Herleitung etwas komisch, und kenn mich da auch ned 100% aus ^^
Die freiwerdende Energie/reingesteckte Arbeit ist einfach das Integral über die Kräfte*Weg