Also ich hab mir das Bsp nochmal durchgedacht…
Bin wieder auf (ω2)^2=(2*K/m) gekommen, da durch die Subtraktion der (g/L)-Term weg fällt.
sagmal wie kommst du bei dem integral beim dreier bsp auf 1/2 ? ich habs jetzt in maple und zu fuß nachgerechnet und da kommt mir als mittel über eine periode irgendwas raus… aber nich 1/2
LG
Uh, ich hab noch was vergessen dazuzuschreiben: T=2pi/ω
Dann sollte es lösbar sein und 1/2 rauskommen, zumindest wirft mir Mathcad das raus. (ist also anscheinend unabhängig von kz)
Noch ne Anmerkung: Ich hab das nicht händisch integriert, da ich nach gefühlten 1000 mal Int(sin(x)²)dx berechnen einfach schon weiß was rauskommt.
Nur ich hab unabsichtlich die falsche Lösung für Int(sin(ωt-kz)²)dx hingeschrieben, bitte das zu ignorieren, das stimmt natürlich nicht, da kommt was viel Ungemütlicheres heraus, das aber auch 1/2 ergibt.
Mir wurde gesagt, dass wir uns für die Tests diese und nächste Woche eventuell die allgemeine Dopplerformel anschauen sollten…
f_B=f_S\frac{c\pm v_B}{c\mp v_S}
(S… Sender, B… Beobachter, c… Schallgeschwindigkeit im Medium)
ich kann euch sagen, dass (zumindest wars beim ersten Test letzte Woche so) haarscharf das gleiche Beispiel zum Test kam als letztes Jahr zum erstn Test. Leider habe ich mir die Testbeispiele vom letzten Jahr nicht notiert, das wäre heuer Gold wert - kann die wer organisieren? 
LG
Hier meine Lösung zu Beispiel 3, mit etwas anderem Ansatz
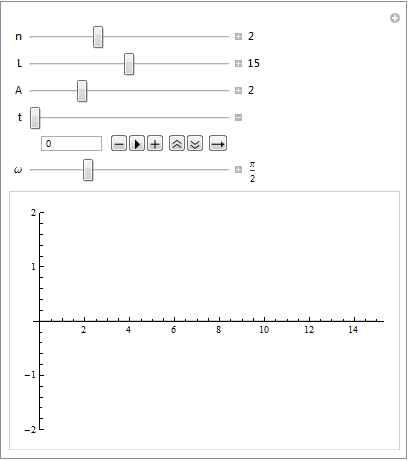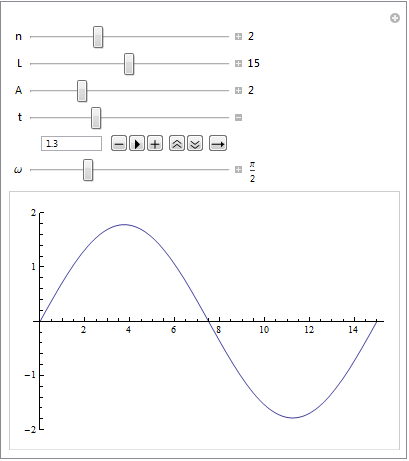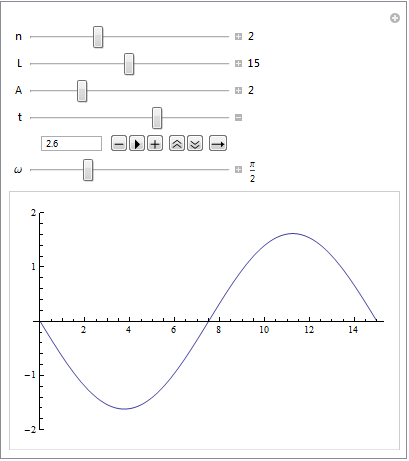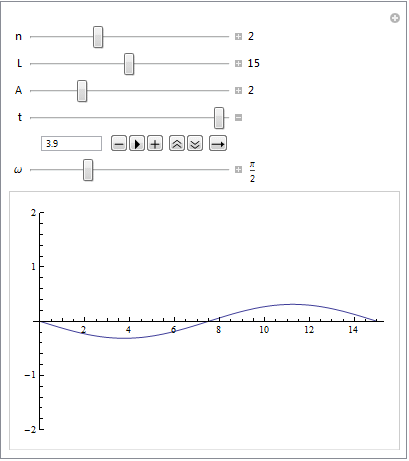
beispiel3.pdf (192 KB)
Zum Beispiel 6: Um auf die Lautstärke zu kommen brauch ich doch die I[min] von 400Hz (in der Lösung wurde mit I[min] von 1000Hz gerechnet)? Wie berechne ich mir die denn am besten?
tach,
also ich mich auch mal ein bisschen im forum umgesehen und folgende lösung gefunden 
https://forum.fstph.at/t/frage-zu-physik-1/596/12
komm damit (also mit diesem ansatz) auch auf die richtige lösung
schönene abend nu
Habt ihr schon eine Lösung für das 6. Beispiel für morgen?
Wie kann man die Lautstärke bei einer Frequenz von 400Hz berechnen?
Es ist ja alles auf 1kHz genormt.
SEXY 
Sieht sehr gut aus.
Hast du das mit Mathematica gemacht? oder mit einem anderem Programm? ( 
wäre auch für meine Berechnungen interessant )
Nochmal zu Bsp 3:
Man kann es über verschiedene Wege angehen, bis jetzt bin ich auf 3 verschiedene gekommen und es kommt immer dasselbe heraus.
Für die Übung wichtig ist nur dass man seinen Ansatz verstanden hat und ihn begründen kann. (und man sollte sein Integral lösen können )
Ich habe die Hörschwelle als konstanten Wert genommen, da die Empfindsamkeit des menschlichen Ohres für 400-1000Hz annähernd konstant bleibt. (siehe Diagramm unten)
Wenn man wirklich die Hörschwelle bei 400 Hz berechnen soll wäre das ziemlich bled, da ich nirgends eine Formel dafür finde, aber man könnte natürlich interpolieren.
edit: muss noch etwas berichtigen aus von meinen Lösungen:
Bsp 5:
Aus irgendeinem Grund habe ich gedacht dass man f und ω berechnen sollte…
Also man soll die f für die offene und geschlossene Pfeife berechnen, die Formeln dazu sind
Frequenz für geschlossene Pfeife = (nv) / (4l) und Frequenz für offene Pfeife = (nv) / (2l)
Danke! Das gif hab ich in Mathematica gemacht. Die pdf mit einem ganz normalen LaTeX Editor (beherrscht also keine Arithmetik).
Code für das gif, falls es wen interessiert ist im Anhang (Ohne dem Export-Befehl außen herum kann man auch an den Balken drehen 
)
Welche Software verwendest du?
bsp3-gifcode2.txt (562 Bytes)
Danke für die Ausarbeitung - finde ich echt super !
Aber eine Sache muss ich fragen, wie kommst du auf den Ansatz,also Asin (kz) sin(wnt) ?
Wäre cool wenn du noch bis morgen antworten könntest
Cool, hab schon viel Gutes von LaTeX gehört nur noch keine Zeit gefunden mir ein Tutorial zu geben.
Vllt mach ich auch nächstes Semester den Einführungskurs…
Ich mach die Lösungen immer mit Mathcad 15 (oder auch Prime genannt). Ist eigentlich nicht wirklich für Mathematiker (und Physiker) geeignet, aber das hab ich halt in der Schule gelernt.
einführungskurs für latex brauchst ned … die codes sind sehr logisch aufgebaut (auch wenn teilweise mit viel tipparbeit verbunden - natürlich abhängig davon welche software du als frontend verwendest - sofern du ein frontend willst)
ich persönlich verwende „LyX“ (http://www.lyx.org/ bzw. http://www.lyx.org/WebDe.Home). gibts für mac/win/linux.
der vorteil von LyX ist, dass du eine wunderschöne oberfläche hast, die sehr an ein normales textverarbeitungsprogramm erinnert. noch dazu musst du nicht jede formel tippen, sondern kannst die standarddinger wie zb integralzeichen, brüche,… einfach auswählen und editieren
(würde aber eher latex lernen und das alles per hand tippen ^^ geht oft schneller).
fazit: LyX ist ein nettes frontend welches WYSIWYM bietet ^^ riesen tutorial und ein sehr ausführliches handbuch is dabei.
es gibt noch viele andere die sehr zu empfehlen sind. LyX war halt mein fav. ^^
LG
PS: abhängig davon welches OS du verwendest, musst du latex extra dazu installieren - LyX is ja nur das frontend
MAn betrachtet das einfach als stehende Welle: Demtröder Seite 397 → Reflektion am festen Ende:
\xi(z,t)=-2A\cdot \sin(\omega t)\sin(kz)
Und dass ich direkt A statt -2A schreibe, kommt daher, dass ich mit A die maximale Amplitude der Saitenschwingung meine und die ist wenn beide sini den Wert 1 Annehmen.
Mann kann sich die Formel auch anhand der Bewegung des gifs überlegen (dazu muss man halt davon ausgehen, dass sich oberschwingungen so bewegen). an jedem Punkt z\in[0,L] durchläuft die Saite eine Sinusschwingung mit der Amplitude A(z)=\sin(kz), wobei k so aufgebaut sein muss, dass am rechten ende die Amplitude null ist, also \sin(k L)=0und somit kL=n\pi \Leftrightarrow k=n\pi/L für ein n\in\mathbb{N} (geometrie der Nullstellen vom Sinus)
Danke danke ! ich versuch das mal zu verdauen
Bin auch der Meinung, dass man keinen Kurs brauchst, um LaTeX zu lernen. Dokumentation zur syntax findest auf google genug. Du brauschst einen Editor und einen Compiler um loszulegen
Editoren gibt es viele, einfach rumprobieren
Hier eine kleine übersicht 
http://en.wikipedia.org/wiki/Comparison_of_TeX_editors
Ein paar wichtige Vertreter:
LyX: Gut für anfänger, weil man keine preämbels schreiben muss. Pdfs lassen sich sehr intuitiv kreieren wegen der enormen grafischen Oberfläche. Fein wenn man „quick and dirty“ techen will. Ein weiteres plus: Ladet auch automatisch einen Compiler (MikTeX) mit runter, wenn du LyX von der herstellerseite aus Runterladest: Würd ich an deiner stelle also als erstes antesten.
TeXnicCenter: Kompelliert selbst bei moderat schlimmen syntaxfehlern. Gewissermaßen der brute-force Editor. Is bei unsrem Latexkurs (Computerstatistik) auch verwendet worden - was auch immer man davon halten soll 
TexMaker 3.1: (mein Favorit). Kann die Arbeitsfläche in 2 Teile teilen: 1 mal die Pdf und 1 mal der Ganz normale Editor → Beim Kompellieren springt er im PDF immer zu dem Teil, den du gerade bearbeitest ohne ein neues Fenster zu öffnen. Ist also super um neue befehle oder packages auszuprobieren, bzw für feinformatierungen.
TeXstudio: Extrem gute Sntaxhighlights und Strukturübersichten. Der proffesionellste den ich bis jetzt kenn aber für Anfänger vielleicht nicht die beste wahl.
Was auch praktisch ist: du kannst files von Mathematica (oder Maple, Matlab, …) in .tex zu exportieren und das file dann mit einem TeX-editor nachzubearbeiten.
Als Compiler würd ich MikTeX verwenden, der hat einen packagemanager (vergleichbar mit synaptic): Also wenn du neue „Makros“ brauchst, kannst du die direkt über den suchen und installieren.
MikTeX is wööödklasse
Für die 3.Übung:
Angabe:
ANG220312.pdf (35.5 KB)
Lösungen:
ANG220312-Lösungen.pdf (103 KB)
Bemerkungen:
- Bsp 1.b. habe ich die Begründung einmal weggelassen, da mir bis jetzt keine passende Formulierung eingefallen ist.
- Bsp 6: Keine Ahnung ob das stimmt, ich habe einfach mal ausprobiert und das ist dabei herausgekommen… Alternativen sehe ich gerne