Los gehts, mit angabe
aufgabenblatt08_ss2010i.pdf (51.5 KB)
holy sh*t, hat noch niemand was gerechnet? ohje ohje… ^^
also ich krieg bei 1a statt dem „mü“ den realteil des imaginären brechungsindex des mediums… hat das sonst noch wer?
kannst du mir bitte sagen, wie du 1a angegangen bist? ich weiß leider nicht so recht, wo ich anfangen soll und was als vorausgesetzt angenommen werden kann und was hergeleitet werden muss…
ich hab mich da an den demtröder 2 gehalten. da wird auf seite 237 der reflexionskoeffizient an metalloberflächen berechnet. ich dachte mir bei beispiel 1a ist ein leiter/also metall gemeint, also müsst das ja passen. beim demtröder kommt aber statt dem mü der brechungsindex raus…
hat sonst noch wer tips zu den restlichen beispielen?
bin am überlegen, das ganze zu boykottieren, is ja echt mal ein beschissener satz an beispielen. finde das total unnötig, uns so sinnfrei zu quälen.
bin am überlegen, das ganze zu boykottieren
ich würd das auch gern machen, weil diesmal hab ich von den beispielen irgendwie überhaupt keinen tau…
war nur schon 2x verhindert und kann mir noch mal nix kreuzen schon fast nimmer leisten… 
diesmal gabs ja auch kein tutorium das ein bisl weiterhilft.
sehr zach…
meinst du, dass dir statt µ n an dieser stelle rauskommt?
ja, das mein ich
hat irgendwer eine ahnung? ich hab keine
hmm…
greiner 315 und die seiten davor fürs 1a
allerdings blick ich trotzdem noch nicht 100% durch
hmm, hab keinen greiner daheim, muss ich mir morgen vormittag noch anschaun.
hat sonst irgendwer irgendwelche ergebnisse?
totally agree
bisher wars je wenigstens immer so, dass die wirklich harten beispiele kombiniert waren mit zumindest einem „nachdenkbeispiel“, welches sowohl an aufwand als auch an umfang geringer war als die harten beispiele.
meine hoffnung is nur dass unser cooler tutor das ganze etwas entschärft, weil nachdem ich mich ein bissl umgehört hab, hat ja wirklich kaum jemand irgendetwas…
nur heißer tip für alle die einen langsamen und genauen tutor haben: 1a) rechnen und alle 5 kreuzeln weil bis dreiviertel zwölf geht sich nie und nimmer mehr als das erste aus :DD
ah ja und @ typhon: das mit morgen vormittag kannst knickn… jedes einzelne beispiel is mindestens 2-6 seiten lang 
hf @ abschreiben
besonders das zweite is ja ein schlechter witz
hast du bsp1 ausm greiner einfach abgeschrieben oder kann man das tastächlich mit den folien lösen? naja ich glaub ich lass es jetzt bleiben xD 4h probiert und nix dabei rausgschaut heist dann wohl dass es net wirklich noch was bringt
lg
ich würds ja abschreiben, aber ich weiß nicht wo…
also 1a im greiner hab ich mitgekriegt, aber wie ich die anderen lösen soll weiß ich einfach nicht. meine ansätze führen zu nichts.
ich probier jetzt sicher seit 5 stunden rum (greetz an calon) aber ich hab einfach garnix weitergebracht.
na wie auch immer.
ahja, falls es jemanden gibt der ein beispiel reinstellen kann/will, würds mich sehr freun, weil ich von den kreuzen her eh sehr knapp drann bin (nicht aus faulheit, sondern weil ich mir schwertu)
lg
zu 8.2a:
Tangentialkomponenten des E und H Feldes an der Grenzfläche müssen jeweils stetig sein.
Ich erhalte folgende Anschlussbedingungen:
E_1^+ - E_1^- = E_2^+ - E_2^-\
n_1(E_1^+ + E_1^-) = n_2(E_2^+ + E_2^-)\
E_2^+e^{ik_2d} - E_2^-e^{-ik_2d} = E_3^+e^{ik_3d}\
n_2(E_2^+e^{ik_2d} + E_2^-e^{-ik_2d}) = n_3E_3^+e^{ik_3d}
Am Ende habe ich ein falsches Vorzeichen erhalten, das dürfte aber wohl ein Rechenfehler in der etwas längeren Rechnung gewesen sein 
Bsp. 8.1 a
Achsenbeschriftung: x nach rechts, y nach oben → tangential = x-z Ebene
Vielleicht kanns ja noch wer brauchen.
lg
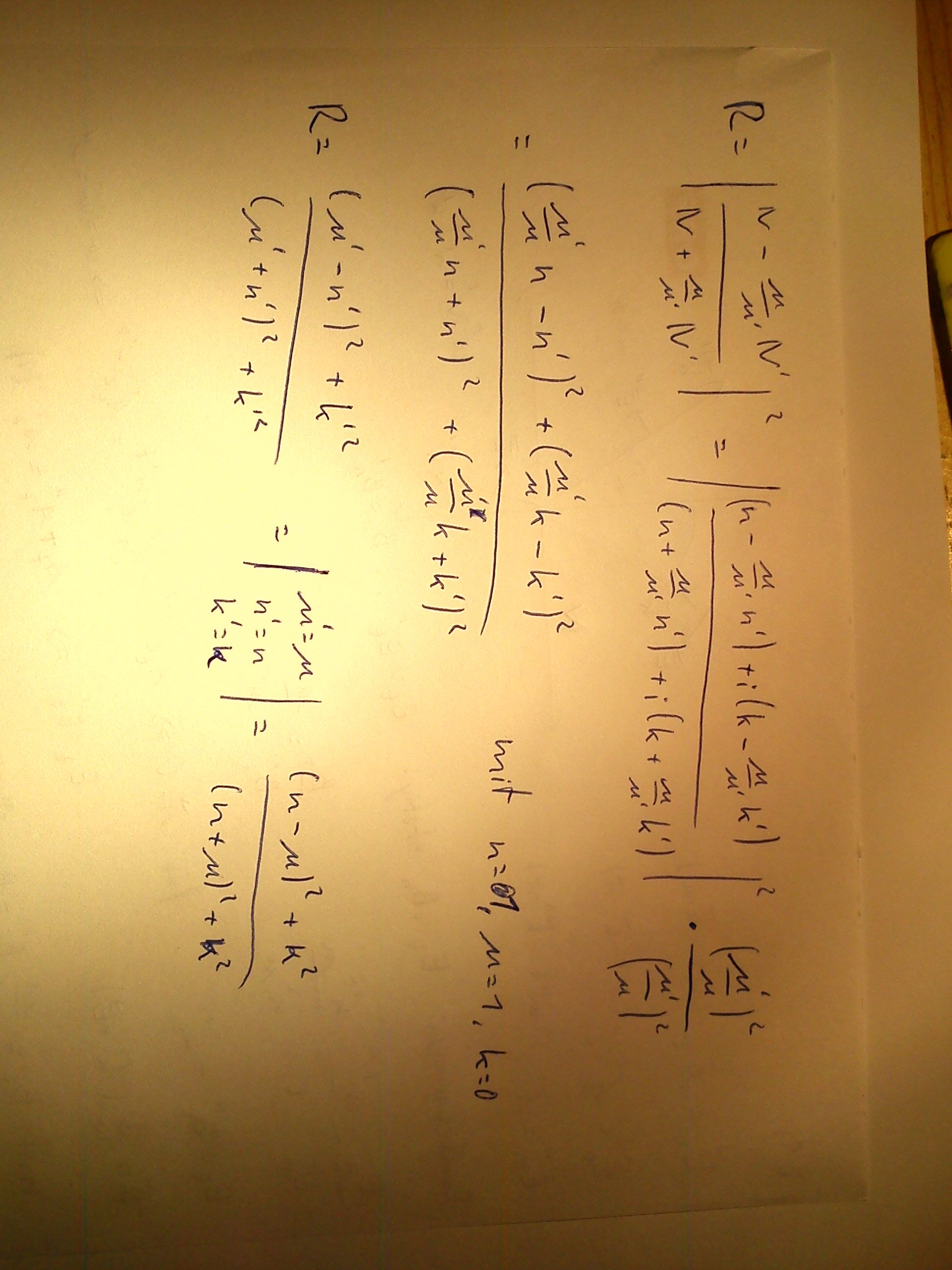
super, ich kanns brauchen
Kann jemand die Lösung von Bsp2 online stellen? Ich rechne schon seit Ewigkeiten herum… ich bin knapp vorm Ende, schaff aber den Durchbruch nicht…
Es werden wahrs. nicht mehr viele am Rechnen sein, aber so stimmts:
E_1^+ + E_1^- = E_2^+ + E_2^-\
n_1(E_1^+ - E_1^-) = n_2(E_2^+ - E_2^-)\
E_2^+e^{ik_2d} + E_2^-e^{-ik_2d} = E_3^+e^{ik_3d}\
n_2(E_2^+e^{ik_2d} - E_2^-e^{-ik_2d}) = n_3E_3^+e^{ik_3d}