Ein Wahnsinn, so schnell war nen Tut noch nieee oben =D>
Wollte nur drauf aufmerksam machen, sodass hochoffiziell vermerkt bleibt ![]()
tut2009_10.pdf (55.4 KB)
einerseits wow, andererseits hätt ich auch drauf verzichten können ![]()
bsp 1)
l = 1 → m = -1,0,1
a)
L_{x}|l,m>=\frac{1}{2}(L_{+}+L_{-})|l,m>
L_{x} = \sum_{m, m’ = -1}^{1}\frac{1}{2}(L_{+}+L_{-})|l,m><l,m’|
[0 1 0]
[1 0 1]\frac{1}{\sqrt{2}}\hbar = L_x
[0 1 0]
b)
Eigenwert
\lambda = \hbar, 0, -\hbar
Wie genau müssen wir 2a aus rechnen?
Reichst es, wenn man den erwartungswerte von H berechnen und gleichsetzten mit \Delta E = hf, oder müssen wir auch den Bahndrehimpuls zusätzlich zur Energie betrachten?
Fürs 1) erhalte ich dieselb Matrix & EWs.
Ich nehme an, wir befinden uns in einem Eigenzustand zur Energie, d.h. \Delta E=0, od. meintests du \Delta E_{21} - dann ja.
Wieso Bahndrehimpuls, wir befinden uns doch in keinem Magnetfeld, es liegt Energieentartung vor!?
Ich hätte einfach die Rydberg-Ritz Formel verwendet \frac{1}{\lambda}=R_\infty(1-\frac{1}{4}) \Rightarrow \lambda_{21}=121,6\ nm was eben dem 1.Strich in der Lyman-Serie entspricht.
Aber aufpassen im Skript ist nicht R_\infty sondern die Rydberg-Energie gegeben mit R_y=h c R_\infty
EDIT: Ok, die Frequenz war gefragt, dann ist es \nu=\frac{R_y}{h}(1-\frac{1}{4})=2,47\ 10^{15}Hz
Zu 2b) Ist Bsp 9.6b (S.409) im [Grau].
Im Burgdorfer Skript findet man diese Formel auch und dort ist das „Ry“ gleich als die Rydberg Energie angegeben mit 13,6 eV.
Führt auch auf diese 2,47 * 10^15 Hz.
irgendwas mach ich da anscheinend falsch, wie kommt man von L_{x} = \sum_{m, m’ = -1}^{1}\frac{1}{2}(L_{+}+L_{-})|l,m><l,m’|
auf die matrix?
Das m und m’ sind eigentlich das gleiche m über die Summiert wird. Du bekommst dann eben 3 Ausdrücke auf welche die Leiteroperatoren dann wirken (dadurch dass auf den m=0 beide ungleich 0 werden bekommst du dann 4 Matritzen welche du addierst).
Du hast zb Ausdrücke wie |10><11| (mit nem vorfaktor halt) und jetzt legst du halt zb fest dass
|11>=\begin{pmatrix}
1\
0\
0
\end{pmatrix}
|10>=\begin{pmatrix}
0\
1\
0
\end{pmatrix}
|1-1>=\begin{pmatrix}
0\
0\
1
\end{pmatrix}
bzw kannst es der übersicht halber halt erstmal |1> |2> |3> nennen.
Denn wenn du zb stehen hast |10><11| = |2><1| kannst du ablesen 2te Zeile 1ste Spalte, genau dort kommt der Eintrag dann hin.
Für 2c bekomme ich:
|\Psi_{n00} (0)|^{2}=\frac{1}{\pi n^{3}a^{3}}
Was maximal ist für n=1 → K-Schale.
Versteht jemand das 2b? Hab das im Grau zwar durchgelesen aber das hilft mir nicht wirklich weiter ![]()
Ich hab bei 2.c. schlussendlich auch das Ergebnis, dass bei n=1 die Aufenthaltswahrscheinlichkeit am größten ist, nur schaut mein Ausdruck etwas anders (=komplizierter) aus.
Wie hast du das gerechnet?
Ich habe die fertige Lösung der Schrödingergleichung in Kugelkoordinaten genommen. Dort sieht man gleich mal dass sie nur für l=0 ungleich 0 werden kann was mir auch gleich m=0 liefert. Dann das Betragsquadrat mit einer Deltafunktion um den vektor r = Nullvektor unter dem Integral, alle Winkelabhängigen Teile sind nur l=m=0 bereits weg, die Kugelflächenfunktion ist eine Konstante geworden (kann man aus ner Tabelle ablesen, zb Demtröder), für das komische L kann man dann nach Angabe „n“ einsetzen, über Deltafunktion integrieren und dann bleibt das stehen. Bzw zuerst hab ich nur das Betragsquadrat um den Punkt ausgerechnet aber wenn man die Wahrscheinlichkeit dann mittels Delta rechnet (geht ja nur um einen Punkt) bleibt wieder nur das Betragsquadrat stehen das eben so ausschaut.
Ich werd das am Abend vieleicht schonmal reinstellen, aber jetzt keine Zeit mehr.
Ich hoffe nur jemand steigt bei dem 2b durch weil das im Grau ist ja wirklich komplett theoretisch >_>
mein 2c sieht so aus.
(erste Seite nur direkt das Betragsquadrat umgeformt, 2te Seite unterm Integral gezeigt dass die Dichte und die Wahrscheinlichkeit in diesem Fall gleich aussehen da es nur um einen Punkt geht)


Der Rest auch gleich. Nur 2b fehlt noch.

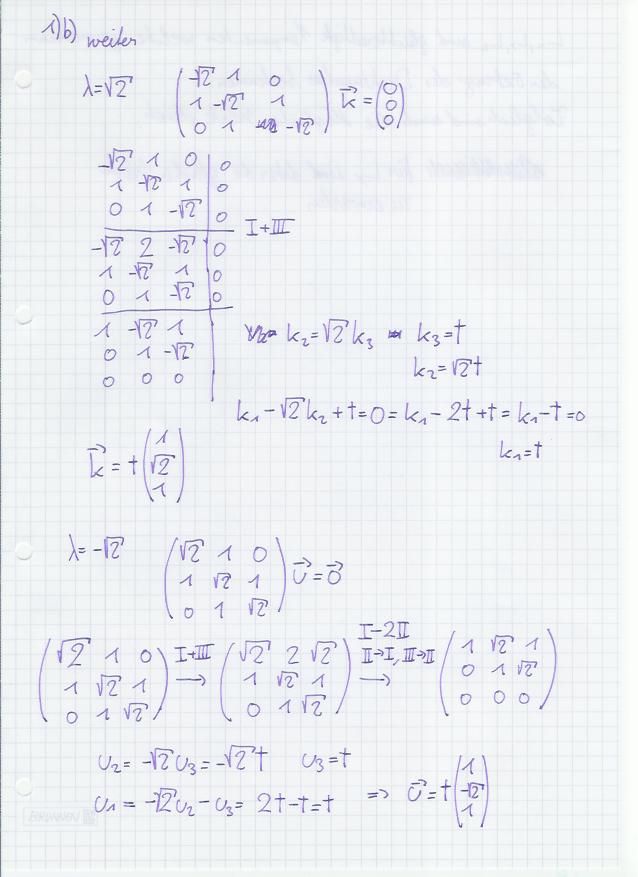


Also jetzt mal ganz auf blöd, weil das Beispiel ist ja nichtmal ein eigener Punkt, kann es sein dass er den Erwartungswert garnicht explizit sehen will sondern nur hören will dass nur ein Moment existiert wenn ein ungerader zustand mit einem ungeraden multipliziert wird (=ungerade) und durch das r dann eine gerade Funktion wird?
zu 2b)
\Delta m = -1,1,0 <= folgt aus dem integral über phi abhängigkeit
l+l’ = ungerade <= folgt aus der Parität
\Delta l = 1,-1 <= folgt aus integral über theta abhängigkeit mit P^{m}_{l}
wenn man nur <nlm|d|nlm> lösen müssen, ist der erwartungwert 0, da 2l = gerade.
mit <n’l’m’|d|nlm> muss man noch folgende integralen lösen:
\int_0^{\infty}!R_{n’l’} R_{11} R_{nl}
\int_{\Omega} !Y^{*}{l’m’}Y{1\mu}Y_{lm}, d\Omega mit \mu = -1,0,1
ok, dann wollen wir mal…




Frage 2b @Lelouch
Erstens, danke für die ausführliche Rechnung =D>
Aber wieso berechnest du Übergangswahrscheinlichkeiten Übergangsdipolmomente, wenn doch nur EW des Dipolmoment eines Zustands |n l m> gefragt ist.
m.M.n braucht man nur das Argument mit der Parität, d.h. nur der erste Teil von 2b.jpg ![]()
Ich glaube zwar auch dass lediglich der erste Teil gefragt war (also Seite 1) aber ich dachte mir es schadet nicht das zu vertiefen und falls er doch mehr hören will hat man was zur Hand.
Was in dem Fall natürlich etwas blöd ist und mir gerade auffällt, ist dass man sich hier ja auf 2 pure Zustände festlegt (keine Überlagerung). Wenn man es mit Überlagerungen rechnet müsste man auch wieder für jede die Paritäten anschaun.
Anhand der Übergänge lassen sich einfach diese Bedingungen für m und l leicht herleiten und physikalisch erklären.
Im Nachhinein betrachtet reicht es wohl einfach die jeweiligen Kugelflächenfunktionen für die Eigenzustände anzuschaun und dort die Relation dass l+l’ = ungerade sein muss zu sehen.
Ich muss halt auch sagen ich verstehe bei dem Beispiel generell nicht ganz, was und wie genau, wer es jetzt hören will. Da ist es besser man geht einen Schritt zu weit als einen zuwenig.
HallO!
…Bin ich da richtig, wenn behaupte, dass die abgestrahlte Frequenz im Bereich der „starken UV-Strahlung!“ liegt?
lg
Hallo!
Also wie argumentiert ihr, dass die Eigenwerte von Lx die selben sind wie für Lz?
Natürlich ergibt sich aus dem obrigen, dass das auch für Ly gelten muss, da sowohl Lx als auch Ly auf Lz orthogonal sind…aber slebst dass scheint mir etwas schwach zu argumentieren!?
Kann mir da wer helfen?
Danke!
Naja hat er ja immer selber gesagt. Man wählt sich einfach die z-Komponente, hätte aber genauso die andern beiden nehmen können. Physikalisch sind alle 3 gleichberechtigt und daher müssen sie die gleichen eigenwerte haben da eine Messung ja einen der Eigenwerte ergibt. Hätte eine Komponente einen eigenwert den die anderen nicht haben würd das diese gleichberechtigung zerstören.
ich hab ihm heute auch mein 2b gezeigt und er will diesen vergleich zwischen l und l’ garnicht, sondern gefragt is nur für gleiche n l m, dh dass das Moment in dem Fall 0 wird. Sprich ungerade Funktion über symmetrisches Intervall bzw über die Kugelflächen zeigen. Also im Endeffekt eh ein geschenktes Beispiel.
Vieleicht schreib ich das nochmal genauer zusammen, aber eigentlich erfüllt die erste seite vom 2b von mir das beispiel. falls mans über die kugelflächen zeigen will halt noch ähnlich wie auf der 2ten seite ansetzen dann hat mans nochmal schön über diese funktionen gemacht.