Hallo!
Kanns sein, dass bei 1b das charakteristische Polynom \lambda ^3 - 2 \lambda ist??
Ok, sry, kommen eh die gleichen Eigenwerte raus 
ja ist es. Das führt ja dann gerade auf die Wurzel(2) Eigenwerte. Für die Eigenwerte musst du aber den Vorfaktor noch berücksichtigen (am einfachsten einzusehen mit der Spur) was dir dann 0 und ± das reduzierte Wirkungsquantuum liefert.
Zu 1b gleich noch:
Die Eigenvektoren müssen natürlich normiert werden, aber das schreib ich normal nicht hin. Nur falls sich wer wundert.
Und warum setzt du dann beim Eigenvektor-Ausrechnen als Eigenwert \sqrt{2} ein, und nicht \hbar??
Weil \sqrt{2} der eigenwert der MATRIX ist, aber der OPERATOR noch den vorfaktor hat. Die Wurzel ist Eigenwert der Matrix, aber nur ein Teil des Eigenwerts des Operators.
Man kann das ganze ja sicher berechnen indem man den Vorfaktor in die Matrix rein schreibt, aber dadurch wirds nur unschöner zum schreiben/rechnen.
Um das formal schön zu schreiben hab ich am Ende eben die Spur berechnet. Die ist ja dann einfach der Vorfaktor mal der Summe der Matrix-Eigenwerte. Dort fällt dann überall die Wurzel weg und ±\hbar und 0 bleiben.
Wenn man das beim berechnen hineinzieht müsste der Vorfaktor beim normieren dann sowieso verschwinden, wenn ich das grad richtig durchdenke. Der wirkt für den Vektor ja lediglich als ein skalarer Faktor aber als Komponente.
Fragen zu 2b) (von Lelouch):
- Was ist dein Denkansatz das (fixe?) vektor-d zu einem Operator zu machen, der anscheinend über alle möglichen Positionen läuft? Blicke da bei dem Beispiel nicht durch.
- Dein Operator R hat Eigenwerte die Vektoren sind, das ist mathematisch gesehen sehr gewagt bzw macht so einfach keinen Sinn. Wie ist das zu interpretieren?
Der ganze Erwartungswert ist ein Vektor, also ein Vektor dessen Komponenten Erwartungswerte sind. Man kommt auch zu dieser Form wenn man einfach 2mal die Einheitsmatrix einschiebt. Der Vektor lässt sich heraus ziehen (macht ja keine unmittelbare Operation mit den Bra-Kets weil er ja aus x,y,z besteht, genau wie mim Ortsoperator der das x liefert welches ich dann hervorziehen kann) und durch das innere Produkt in der mitte bekomme ich wieder eine Delta-Funktion für eines der Integrale. Durch das Umschreiben wie ichs gemacht habe gehst du quasi einen schritt zurück und sparst dir halt einfach ein bisschen Schreibarbeit weil du das 2te Integral garnicht erst hinschreiben musst.
Es sind also auch keine Vektor-Eigenwerte sondern es sind einfach Komponenten in ein lineares Gleichungssystem zusammengefasst da du eigentlich 3 Zeilen hast.
Ich hab das auch mit den 2 Einheitsmatritzen inzwischen geschrieben, ich lad das die nächsten paar Minuten mal hoch.
Der Ansatz mit dem Operator war einfach quasi einen Schritt zurück zu gehen und einen allgemeinen Operator mit Spektraldarstellung im Ortsraum hinzuschreiben um so das Beispiel etwas zu kürzen. (So haben wir es auch damals gemacht als wir die Delta-Funktion in den Impulsraum übertragen wollten).
ok, ist schon ein bisschen klarer, bin mit dieser physiker-schreibe nicht so vetraut 
danke fürs uploaden und die mühen!
Es is sicher net die schönste Schreibweise, aber ich sehe es eben als so ein System an. Das Dipolmoment ist ein Vektor, daher muss der Erwartungswert auch ein Vektor sein. Man kann das natürlich einzeln für alle Komponenten hinschreiben, aber man gewinnt dadurch nix ausser mehr Schreibarbeit. Der \vec{r} Vektor ist ja kein Operator mehr (besteht ja aus den Komponenten x y z) daher kann man ihn in jeder Gleichung aus den Bra-Kets rausziehen. Verwechseln darf man halt nicht dass hier die Bra-Kets natürlich nicht direkt auf den r Vektor wirken sondern auf die Komponenten (vieleicht am besten einklammern um das nicht zu verwechseln? keine Ahnung wie man das besser notieren sollte), würde man die Bra-Kets direkt mit dem \vec{r} wechselwirken lassen kommt natürlich n Blödsinn heraus. Die ganze Spielerei kann man sicher aber sicher sowieso sparen weil man ja das Betragsquadrat von Psi bekommt (gerade) und mit einer ungeraden Funktion (ort) multipliziert und das wird natürlich 0.
Achja vergesst das mit dem I=-I=0 unten am besten, is wohl blödsinn. Wichtig is nur dass die Funktion halt ungerade ist.
Ich hätte es so wie im Grau 2.6 gemacht:
Was sagen die Experten dazu?
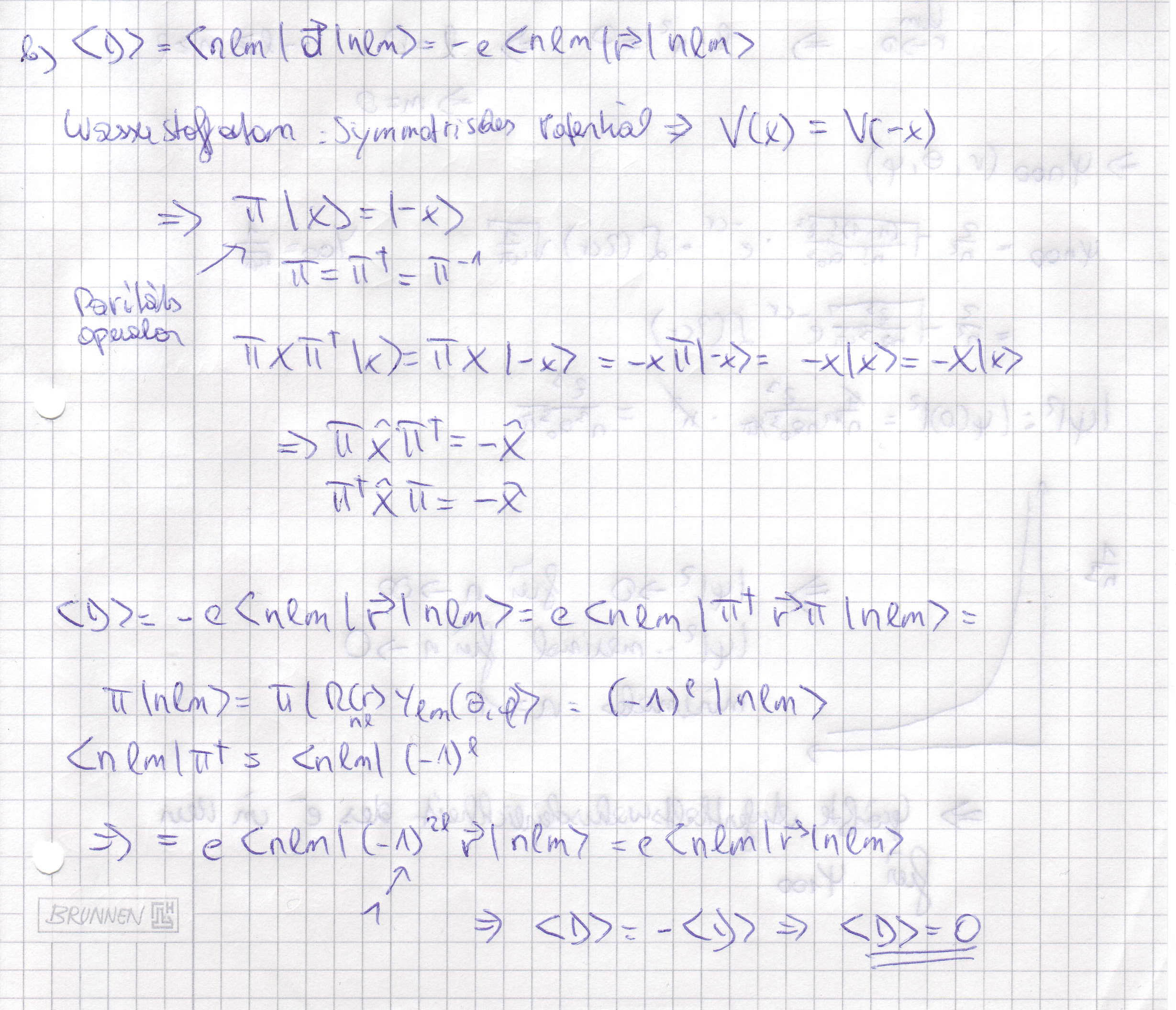
Würde ich eigentlich auch sagen dass es stimmt.
Das einzige wo man vieleicht was bemängeln könnte ist dass direkt das Bra/Ket gedreht wurde ohne Basis bezug. Ob das allgemein erlaubt ist oder nicht weiß ich jetzt auch nicht, aber es scheint auf jeden Fall zu funktionieren.
verstehe die 4. zeile von unten nicht.
Hm ja stimmt die ist problematisch weil da auf Ortskoordinaten festgelegt und nicht mehr Basisfrei 
Edit: bzw festgelegt stimmt nicht, es wird einfach so ins Ket geschrieben. Wie gesagt ich bin mir net sicher ob man es direkt so spiegeln darf.
Ich habs halt in die Ortsbasis gelegt damit ich die Kugelflächenfunktionen betrachten kann. Nachdem er auch heute in der VO auf die Kugelflächenfunktionen verwiesen hat glaube ich auch dass es wirklich so gedacht war. Ob man es irgendwie direkt am Ket sehen kann… keine Ahnung. Ich wüsste so jedenfalls nicht welche Parität die Funktion hat also glaub ich langsam man kanns doch net so sagen.
Wenn ich nun auch eine Vollständige 1 einschreibe mit Integral über r wärs ja wieder das gleiche wie die Lösung von Lelouch denk ich. Na mal auf morgen warten. Ich wäre Dankbar wenn jemand die korrekte Lösung dann morgen posten könnte, da ich beruflich bedingt nicht ins Tutorium kommen kann.
Dankeschön
Unser Tutor hats in Bra-Ket gezeigt, also darf man es wirklich so machen.
Am meisten hass ich ja, dass es wieder in jeder Gruppe irgendwie anders ausschaut…
Wieso wie schauts in anderen Gruppen aus?
In Bra-Ket ging das bei uns einfach:
<nlm|\vec{r}|nlm>=<nlm|\Pi^{\dagger } \Pi \vec{r}\Pi^{\dagger } \Pi |nlm>
(-1)^{2l}(-1)<nlm|\vec{r}|nlm>=(-1)<nlm|\vec{r}|nlm>=0
@Lelouch: Ergänzung 2c) (hat mich sehr verwirrt ):
Es kommt nicht |\Psi_{n00} (0)|^{2}\ne\frac{1}{\pi n^{3}a^{3}} heraus.
Da der Vorfaktor der Wellenfunktion korrekt lautet (3-Potenz von (n+l)! im Nenner):
\sqrt{\frac{(2 \kappa)^3 (n-l-1)!}{2n [(n+l)!]^3}}.
Die Verwirrung ist, dass je nach Autor L_{n+l}^{2l+1} und L_{n-l-1}^{2l+1} geschrieben wird.
Die Autoren verwenden hierbei jedoch keine Identitäten mit Faktoren sondern unterschiedliche Definitionen
In erster Form (Kreuzer): L_r^s(x):=\frac{d^s}{dx^s}L_r(x)
In zweiter Form (Burgdörfer): L’{r-s}^s(x):=(-1)^s \frac{d^s}{dx^s}L_r(x).
L_r^s(x)\ \Leftrightarrow\ (-1)^s L’{r-s}^s(x)
Auch die Def. im Kreuzer-Skript ist fehlerhaft, korrekt findet man sie in „Ballentine, Quantum Mechanics - A Modern Development“, S.267.
Also bei uns kam auch im Tutorium genau mein Ergebniss heraus und kein anderes.
das heisst aber noch nichts, wenn z.B. auch die anderen das Burgdörfer Skript verwendet haben…
Noch hinzu kommt, dass in der deutschen Wiki der Faktor auch falsch war, in der Englischen hat er gepasst…