- Tutorium am 13.11…
tutorium3.pdf (47.4 KB)
Liebe Kollegen,
da ich das neue Skriptum vom Prof. Burgdörfer nicht besitze, könnte bitte jemand die entsprechenden numerierten Formeln hier angeben, welche in den Übung verlangt werden?
Danke im Voraus!
Gutes Gelingen
Klaro ![]()
zu 2)
Gleichung 7.17:
\Re(\alpha,\beta,\gamma)=e^{-\frac{i}{\hbar}J_z\alpha};\cdot;e^{-\frac{i}{\hbar}J_y\beta};\cdot;e^{-\frac{i}{\hbar}J_z\gamma}
Mit der Abbildung 7.3 kann ich leider gerade nicht dienen.
Zu 4)
Gleichung 7.23:
d_{m’m}^{(1)}(\beta)=\begin{pmatrix}\frac{1}{2}\left(1+\cos\beta\right) & -\frac{1}{\sqrt{2}}\sin\beta & \frac{1}{2}\left(1-\cos\beta\right) \ \frac{1}{\sqrt{2}}\sin\beta & \cos{\beta} & -\frac{1}{\sqrt{2}}\sin\beta \ \frac{1}{2}\left(1-\cos\beta\right) & \frac{1}{\sqrt{2}}\sin\beta & \frac{1}{2}\left(1+\cos\beta\right)\end{pmatrix}
Ich hoffe ich habe alles richtig abgetippt.
Jannek, danke Dir vielmals!!!
sehr lieb ![]()
gibts ideen, ansätze??? wäre für jeden tipp dankbar!
Hat jemand tipp?.. Etwas kleineres?
na gut dann fang ma mal ganz klein an:
1.) a) und b) steht im prinzip im demtröder III (seite 302, der starre rotator). bei b) steht schätzen weil es sich um ein halbklassisches modell handelt. scheint prinzipiell nichts anderes zu sein als die energiedifferenz zwischen grundzustand und ersten angeregten zustand!
c) da würde ich die energiedifferenz einfach mal mit 1/2*kT vergleichen??
2.) da weiß ich noch nicht ob und wie ich S (J=L+S) einbauen soll oder kann. vielleicht hab ich da aber auch den falschen zugang.
3.) hab ich überhaupt keinen schimmer!!!
4.) in bearbeitung - krieg ich aber hin. sollte mir was richtiges rauskommen stell ichs morgen noch online.
ad 1-4) bitte um diskussion!
wenn jemand was richtiges hat, bitte online stellen!!! ihr wißt ja - gemeinsam sind wir stark ![]()
Wenn die hier von der inneren Energie eines idealen Gases ausgehtst, dann heißt es doch allgemein:
U(T)=\frac{f}{2};k_B;T
wobei f der Anzahl der Freiheitsgrade (hier 6) entspricht. Oder beschränkt man sich gar nur auf die beiden Rotationsfreiheitsgrade?
Oder anders gefragt: warum 1/2?
hier mal meine ideen zu 1.
sorry für die schlechte qualität aber ich hab keinen scanner…
verbesserungsvorschläge nehme ich gerne entgegen!
lg


f ist die anzahl der freiheitsgrade - das ist richtig. wenn du 6 annimmst hättest du aber 3 grade der translation und 3 grade der rotation. ist mir auf jeden fall zuviel. ich hätte deswegen nur einen rotations-freiheitsgrad gesagt weil unser halbklassisches modell ja quasi auch nur einen berücksichtigt (ich würds zumindest so interpretieren). aber um eine drehung in der ebene zu beschreiben bräuchte man aber schon zwei… hm ![]() , weiß ich jetzt auch nicht genau.
, weiß ich jetzt auch nicht genau.
@yourmirror: also was ich da jetzt so überflogen habe, würde ich meinen das passt so (ev. bis auf die anzahl der freiheitsgrade). also ich habs genauso gemacht - nur noch keine zahlenwerte eingesetzt.
also ich find die angabe ist dahingehend unklar, is aber auch egal weil die thermische energie eh großgenug ist ums anzuregen.
ob das dann im 3., 5. oder 10. rotationsniveau ist, ist ja eigentlich auch nicht gefragt und recht egal…
lg
Bei 6 Freiheitsgraden hat ein lineares Molekül 3 Translations-, 2 Rotations- und 1 Vibrationsfreiheitsgrad. Zwar reicht die thermische Energie so oder so aus um das Molekül anzuregen, aber es macht meiner Meinung nach einen Unterschied, da in 1d) nach einem optischen Übergang gefragt ist. Die Energiedifferenz zwischen den Niveaus sind ja gerade nicht äquidistant.
Außerdem ist in 1d) nach einer optischen Anregung gefragt (welches Licht soll erzeugt werden?) und dieser ist, laut Auswahlregeln, nur bei \Delta J=\pm 1 erlaubt. Also ein Übergang aus dem mittleren Anregungszustand in den Nächsthöheren.
Meine Meinung ![]()
Falls du noch nicht mit der Bearbeitung fertig bist, habe das 4a schon! Das 4b) bin noch nicht sicher, ob es stimmt, was ich bis dahin gemacht habe, aber bis am Abend kommt noch…
IMG-4.2.pdf (367 KB)
@gino: ausgezeichnet! dann stell du das 4. bsp. bitte komplett online. ich werde dann noch das 2. beispiel online stellen - das ist mir dann doch recht leicht von der hand gegangen (aber erst gegen abend, bin noch unterwegs).
das is was ich zum 3. hab
quanten II 2009-11-13 3.Bsp.pdf (397 KB)
frage zu 3a:
die zustände aus denen deine dichtematrizen da bestehen sind aber eigenzustände von Jx und nicht Jz oder?
denke das stimmt so…
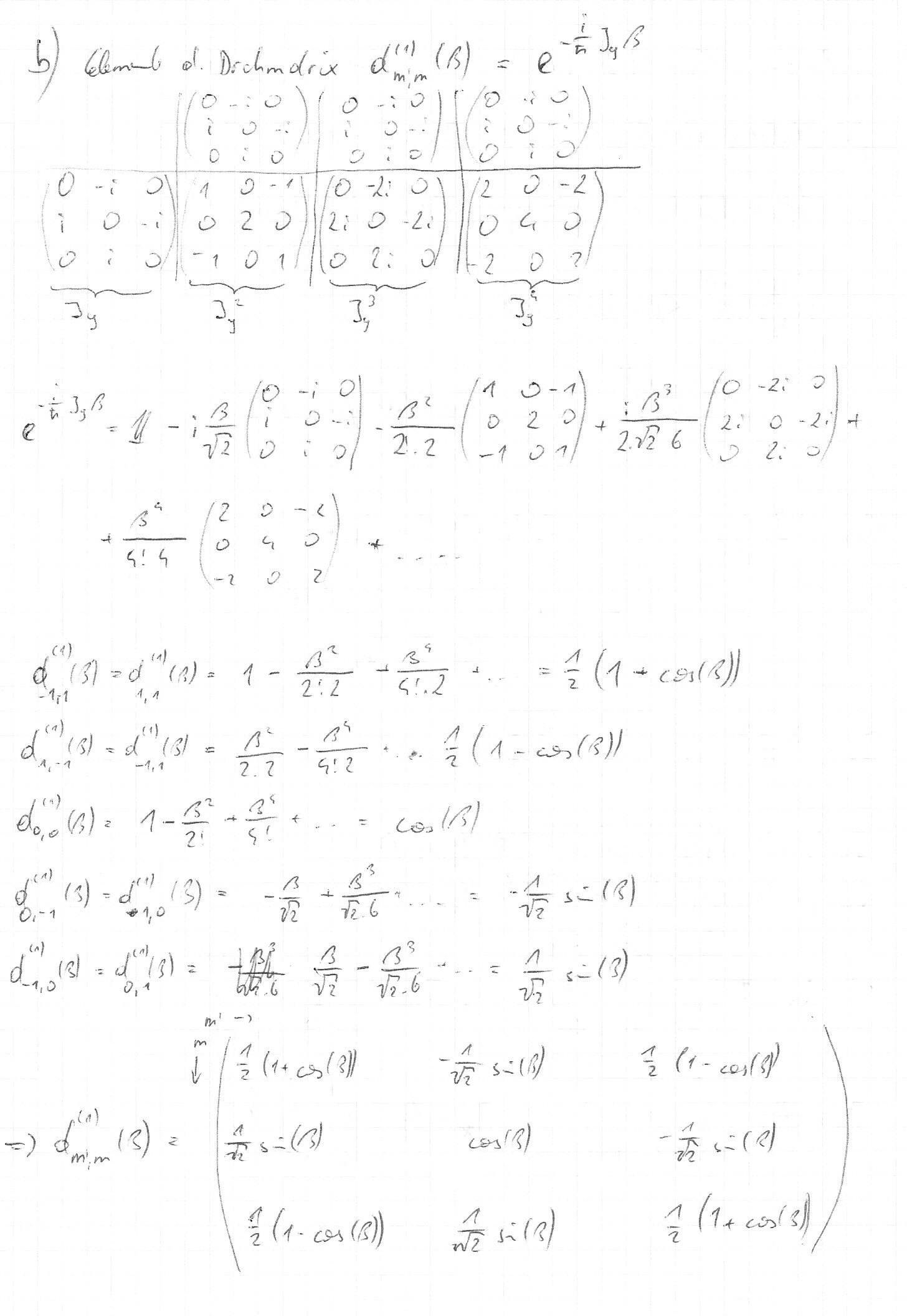
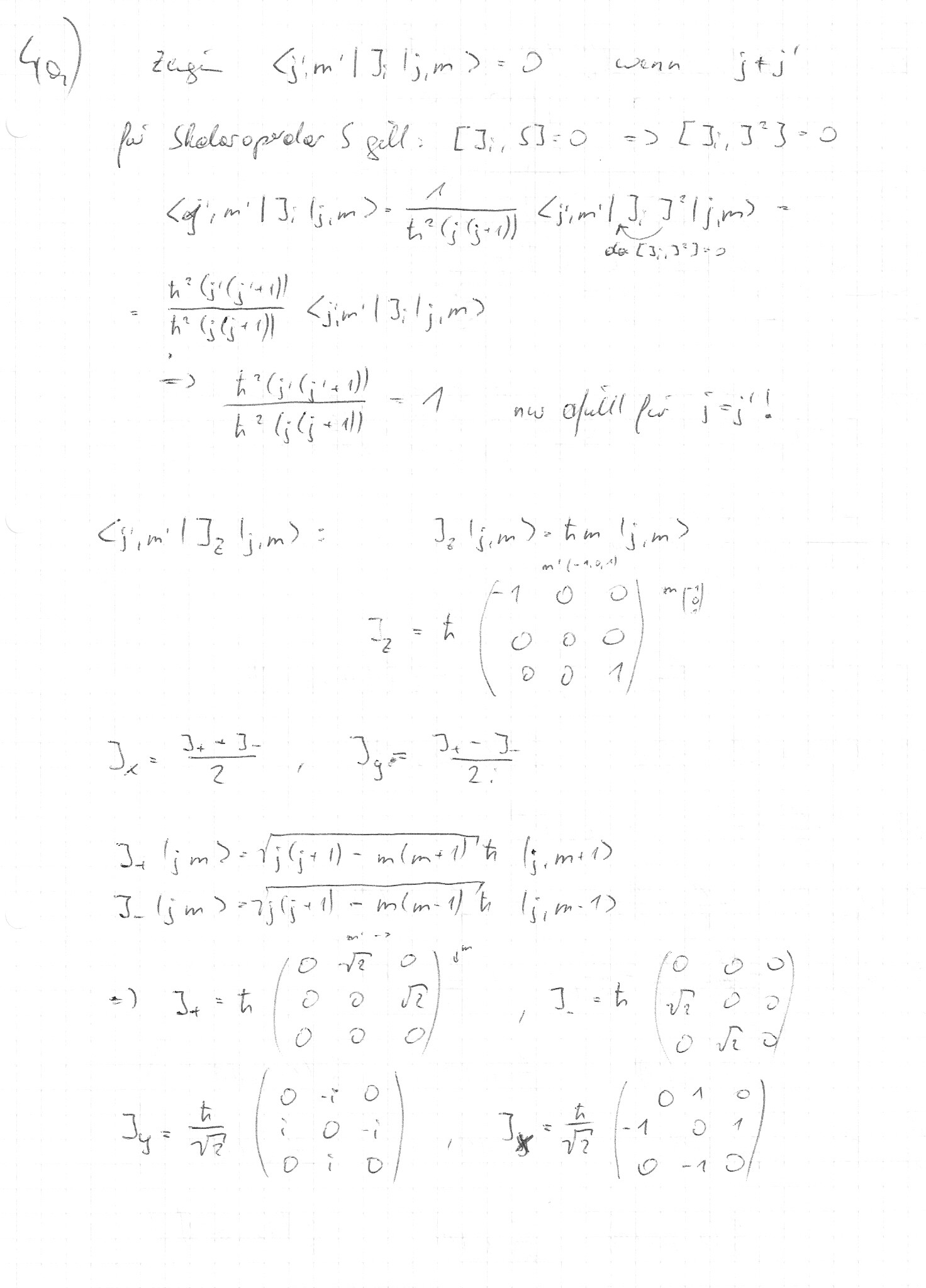
Wie versprochen das zweite Beispiel!
Quanten_2Bsp0001.tif (1.07 MB)
könnte bitte jemand 3c kurz erklären?
danke!
also ich hab 3c so gemacht:
nach dem ersten magneten befindet sich jeder der strahlen (1,2,3) in einem eigenzustand des Jx-operators (jeder der strahlen hat hier noch 1/3 der anfangsintensität). wenn man dann das eigenwertproblem für die Jx-matrix löst kommt man auf genau diese eigenzustände, ausgedrückt in der Jz-basis, also als superposition von Jz-zuständen. was man dann rausbekommt ist dass die strahlen 1 und 3 jeweils aus einer superposition der Jz zustände m=0,-1,1 bestehen bzw. der strahl 2 nur aus m=-1,1
schickt man diese strahlen nun durch ein magnetfeld, das in z-richtung schaut, spaltet der genau diese zustände auf. die intensitäten sind dann durch die koeffizienten vor dem jeweiligen eigenzustand gegeben.
wobei ich mir nicht ganz sicher bin, da das nicht so ganz mit dem hier schon geposteten bsp übereinstimmt.