Die Angabe anbei.
Ich fange mal an zu rechnen, bin wie immer für jeden zusätzlichen Input dankbar ![]() !
!
tut6.pdf (49.8 KB)
Könnte jemand die Lösungen hochladen, oder einen roten Faden zu die Aufgaben beschreiben?
tue mich als IT-ler ziemlich schwer mit dem Mechanik / Kinetik Teil ![]()
Also ich glaub für das erste Bsp. denkst du dann zu kompliziert.
Wenn du es selbst lösen willst lies dir http://de.wikipedia.org/wiki/Harmonischer_Oszillator durch, ansonsten siehe den Anhang für 1 und 3.
lg
tutorium9.pdf (57.9 KB)
lsg_tutorium9.pdf (138 KB)
Hallo!
Nun mal meine Gedanken zu diesem Tutorium; Wobei es sich mehr um Fragen handelt. Vielleicht kann mir hier jemand sie beantworten.
-
Bsp.: Bis auf Punkt d) soweit alles klar. Was für eine Integration ist nach der Angabe zu verstehen?
@ 5465: Vielleicht kann ich dieses Bsp. posten, wenn ich es zu einer „humanen“ Zeit zusammen bringe, schön aufzuschreiben. -
Bsp.: Lässt sich das Beispiel einfach durch einsetzen, sprich die jeweiligen Operatoren auf die Energieeigenfunktion anwenden, lösen/beweisen? Werde das morgen nochmal probieren.
-
Bsp.: @ Claus: Danke für die gepostete Hilfe. Nur wie kommt man da auf das x_0?
c) wurde mehr oder wenig schon in der Vorlesung durchgenommen.
d)-e) Habe ich mir noch nicht so genau angesehen;-)
Insgesamt gesagt: Schon verhältnismäßig lange damit beschäftigt, allerdings wenig Output erlang!
Gute Nacht
Hmm
Das hab ich gar nicht gesehen ![]()
Ich würds grob so probieren:
\hat{H} = \frac{\hat{p}}{2 \mu} ; + ; \frac{1}{2}K(x-x_o)^2 = \propto \frac{1}{2}K(x-x_o)^2
Im Grundzustand sollte das irgendwie so (halt normiert nehmen)\Psi_0(x) \propto e^{x^2} aussehen
Und dann sollten wir irgendwie
<\Psi_0|x|\Psi_0> (?) berechnen
mit
E_{pot} = V(x) = \frac{1}{2} \cdot m \omega^2 x^2
sollten die Integrationsgrenzen für das innere des Potentials bestimmt werden können und dann die Wahrscheinlichkeit berechnen, die WF außerhalb zu finden.
Ist sicher kompletter Blödsinn (und ich habs noch nicht ausgerechnet), aber vllt. hilft es ja wem
lg;&;gn\infty
Ja, also gestern habe ich zu 1 d) schon <\Psi_0|x|\Psi_0> habe ich gestern schon berechnet.
Dazu habe ich die Ortsdarstellung des Energieeigenzustands von 2 als Psi_0 angenommen. Weiß jedoch nicht welche Integrationsgrenzen dann einzusetzen sind!
Von 0 bis x? Da ergibt sich jedoch die Schwierigkeit, dass dann 0 im Nenner stehen würde;-)
Was wird unter „klassisch erlaubter“ Abstand verstanden?
Hat vielleicht noch jemand Antworten auf meine oben gestellten Fragen?
Danke für die Hilfe!
Die Tutorien aus 2010/2011 hab ich schon angeschaut, aber ich verstehe nicht wie man auf die Lösungen kommen sollte.
Btw. 2010/2011 in Tutorium 7 (oder 8 ) sollte sowas sein wie die jezige 2. Aufgabe.
Ich schau ob ich was bis morgen noch schaffe.
Könnte morgen nach dem Tutorium jemand seine Lösungen hoch laden? Bin krank und werd morgen voraussichtlich nicht zur Uni kommen. Wäre echt super.
noch besser wär wenn jemand VOR dem tutorium seine/ihre Lösungen uploaden könnte! ![]()
Bin auch grad am verzweifeln. ![]()
also meine Ergebnisse zu 1 sind:
a)
\omega=\sqrt{\frac{k}{m}}
\nu =\frac{\omega}{2\pi }
b)
E_0=\frac{1}{2}\hbar\omega=34,31 meV
c)
\Delta E=\hbar\omega=h\nu=68,63 meV
\nu =\frac{\Delta E}{h}=1,659*10^13 Hz
\lambda =\frac{c}{\nu }=18,07 \mum
d) keine Ahnung!
welchen wert hast du für m eingesetzt?
die reduzierte Masse:
m=\frac{m_1m_2}{m_1+m_2}=\frac{m_{Cl}}{2}
mit m_{Cl}=5,8871*10^-26kg
also mir kommen beim ersten bsp andere zahlen raus, kanns sein das du dich da verrechnet hast?
Die Zahlen müssten beim redrum passen. Habe auch nochmals alle mit Einheitenkontrolle durchgerechnet und komme unabhängig aufs gleiche Ergebnis.
Zum zweiten Beispiel hätte ich folgenden ansatz per Bild. Leider aber keine Zeit ihn vorm Salsakurs fertig zu rechnen. Sollte jemand von euch Zeit haben probierts mal aus.
Im ersten Versuch ist auch das 2x*H_n bei der Ableitung der Hermitenpolynome herausgekommen. Dann hatte ich einen Fehler. Würde mich interessieren was ihr so bekommt…
mfg. Hofi
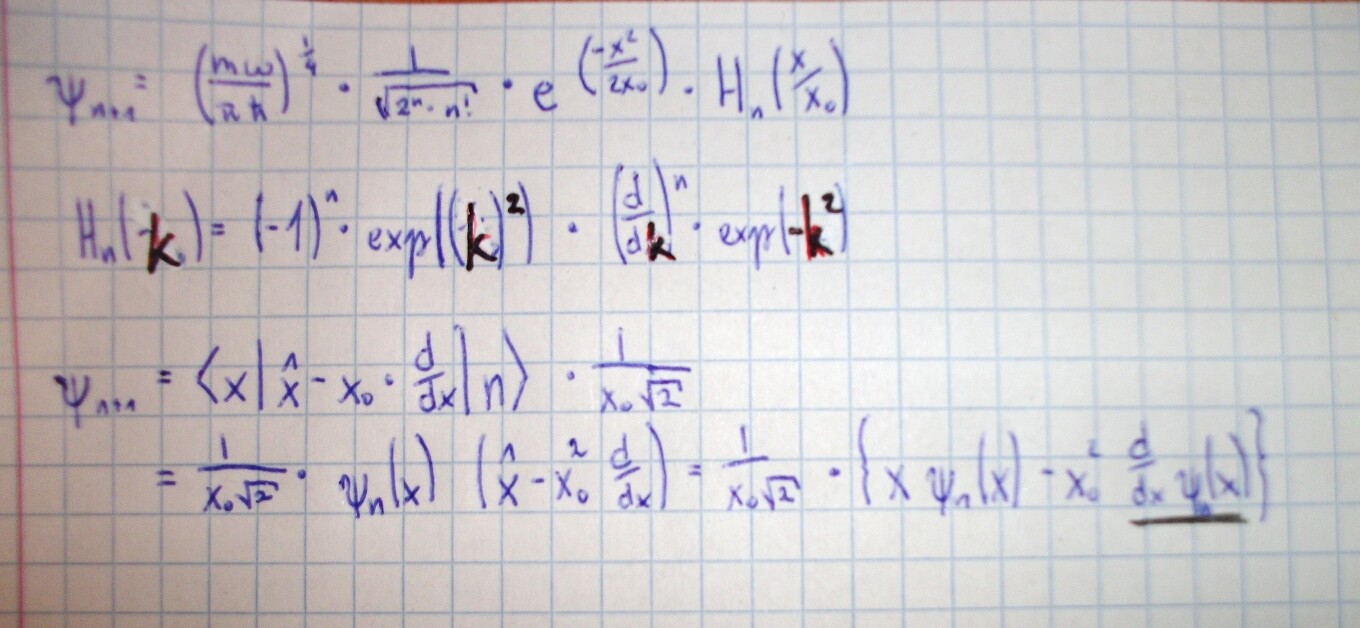

also 1d weiss ich nicht was ich da integrieren soll… und 3b fehlt mir auch noch damit ich wenigstens 2 punkte kreuzen kann… den rest schaff ich nicht, bin für jede Hilfe/Anregung dankbar
Mir gehts echt genau wie dir typhon ![]()
nabend!
da ich glücklicherweise noch immer im büro sitz und noch zu nix gekommen bin … könnt vielleicht wer, der die beispiele mehr oder weniger durchgerechnet hat, diese hochladen?
das wär echt ein feiner zug! ![]()
Seite 4 ist einmal die Energie und das Potential aufgezeichnet.
E=V(x)=\frac{1}{2} m \omega^2 x^2
Da holen wir uns einmal die Grenzen raus, wo wir integrieren wollen, weil wenn wir außerhalb des Potentials messen, gehen wir in den klassisch verbotenen Bereich (die Rechnung ist halt klassisch+qm super gemischt)
x_{1,2} = \pm \sqrt{\frac{2E}{m} }\omega
Die Wellenfunktion aus Wikipedia für den Grundzustand:
\Psi(x)_0 = \big({\frac{m\omega}{\pi \hbar}}\big)^{1/4} e^{-\frac{m\omega x^2}{2\hbar}}
|\Psi(x)|^2 = \int \Psi(x)^\dagger \Psi(x) dx
bei uns:
\int_{-sqrt{\frac{2E}{m}}\omega}^{sqrt{\frac{2E}{m}}\omega} dx sqrt{{\frac{m\omega}{\pi \hbar}}} \cdot e^{-\frac{m \omega}{\hbar}x^2}
Nun das Integral ist nicht so einfach zu berechnen (außer über \pm \infty )
Deswegen einfach mit Mathematica numerisch integrieren:
1 - NIntegrate[kExp[-dx^2], {x, -w, w}]
Die Wahrscheinlichkeit das Teilchen außerhalb zu finden ist natürlich 1minus dem Wert es innen zu finden (Normierung sei dank ![]() )
)
Ausrechnen dürft ihr es selbst ![]()
/e:
Wenn sich jeder beschwert, dass er entweder die Beispiele nicht vollständig hat und/oder nichts hier postet, wird auf kurz oder lang hier Niemand etwas posten ![]()
erstmals danke für die Antwort claus! wenn mein post wie ne beschwerde geklungen hat, dann tut mir das leid… ich bin eher verzweifelt, weil ich die Beispiele einfach nicht hinbekomme
wenn ich in mathematika diese berechnung durchführe dann erhalte ich folgende fehlermeldung: NIntegrate::nlim: x=w is not a valid limit of integration. // kenn mich in mathematica nicht so genau aus, aber das klingt so, als wollte er einen genauen wert als Grenze haben. verwende ich für E die Grundzusandsenergie des harmonischen Oszillatos, sodass x=(hquer/K)^1/2 ist?