Endlich wieder Edyn Übung nach fast einem Monat Pause ![]() . Schaut auf den ersten Blick aber ganz ok aus.
. Schaut auf den ersten Blick aber ganz ok aus.
Tut090508.pdf (46.8 KB)
Hat wer schon die Gesamtladungen bei Beispiel 1 herausen? Ich bekomm da beim integrieren und zusammenzählen immer 0 raus und das kanns ja net sein…
Hab ich leider noch nicht, hätt aber eine Frage zum 3. Beispiel.
Vielleicht steh ich da grad voll auf der Leitung, aber glaubt ihr nicht, dass gemeint, ist, dass das Potential für große y abfällt. Wenn ich mir die Randbedingungen anschau, hab ich ja für z=0 und z=\pi beides Mal V=0. Für y hab ich auf der einen Seite V=V_0, aber für große y keine RB. Für z braucht man daher, denke ich, eine schwingende Lösung und keine Exponentiallösung, abgesehen davon ist das Potential nur für den Innenraum zu rechnen und da kommen keine großen z vor, da z zwischen 0 und \pi liegt. Wie gesagt vielleicht irr ich mich, oder hab die Angabe nicht richtig verstanden.
Glaube ich eigentlich auch, besonders da der definitionsbereich für z schon sehr verdächtig ist und wohl zeigt welche seite der dgl das minus bekommen soll. Mir fehlt nur gerade eine letzte Randbedingung um die Amplitude des Sinus in Z(z) zu bestimmen.
Habe jetzt stehen:
\phi =\sum_{n=1}^{\infty }{\phi_{0} e^{-n y} A sin(n z)}
n ist die seperationskonstante die aus der RB z=pi Z(pi)=0 folgt, damit es für alle vielfachen von Pi gilt.
Edit: OK das rennt wohl auf Fourierkoeffizienten hinaus
So ich denke ich habe das dritte Beispiel nun. Nach bestimmung der Fourier-Koeffizienten ergibt sich für ungerade n (dh schreibe ich die summe auf 2n+1 ausgehend von n=0 um):
\phi (y,z)=\sum_{n=0}^{\infty }{\frac{4\phi _{0}}{\pi (2n+1)}sin((2n+1)z) }e^{-(2n+1)y}
ich bekomm da leider auch nichts gescheites raus, genauso wie bei 2a und 2b… #-o
dabei siehts gar nicht so schwer aus!
2a gerade gelöst. Is wirklich nicht so schwer aber man übersieht es sehr sehr leicht.
Einfach die beiden Terme auf der rechten Seite mal ausrechnen. den n+1 teil 2 mal ableiten (erste mal geht leicht mit Kettenregel, 2tes mal dann Produktregel dazu) und den n-1 Teil garnicht ableiten, da multiplizierst du die ableitung quasi drauf (aus n-1 ableitungen werden n ableitungen). Dann kannst du dir die rechte seite mal vollständig hinschreiben und siehst bei 2 termen gleiche nenner, wobei einer davon ein x^2 dabei hat. da hebst du den nenner und die ableitung der klammer heraus, und siehst dass „zufälliger weise“ nur noch ein (x^2 - 1) die beiden terme unterscheidet. das fasst du wieder von einem l-1 zu einem l zusammen und dann bist du schon fertig. einfach anschaun was heraus kommt wenn du die linke seite ausmultiplizierst (2l kürzen sich, 1 bleibt gleich) und du siehst es is das gleiche. ist aber wirklich ziemliche spielerei. wenn man glück hat kommt man schnell drauf, wenn man pech hat übersieht mans.
Also bei mir kommt bei der Ladung im im Bsp1 -2*\frac{q}{\pi}*arctan(a/b) (bzw a und b vertauscht für die andere Seite) raus → Gesamtladung dann -q (also passt mM)
Beim dritten… warum die Summe? Eine Lösung sollte doch reichen, oder? \phi _{0}*e^{-y}*sin(z)
Ich geh auch davon aus dass die Lösung für große y abfällt und dass des ein Fehler in der Angabe ist (weil für z isses sinnlos)
Die Summe gehört schon hin weil es die Linearkombination aus allen Lösungen ist. das (2n+1) ist der eigenwert aus der differentialgleichung und wir müssen ja die lösung der dgl als eine linearkombination mit allen eigenwerten darstellen.
im endeffekt nichts anderes als bei einer normalen dgl 2ter ordnung nur dass wir diesmal unendlich eigenwerte haben und nicht 2 (± aus der wurzel von lamda).
jaja, Summe stimmt schon, war wohl gestern abend nur zu faul zum denken ![]()
Fourierkoeff. ist dann der vom Rechtecksimpuls (y=0 RB und man erspart sich das rechnen)… das zusammen mit der e-fkt. ist dann ein sehr schönes Ergebnis.
Also ich verlier langsam die Lust, ich bekomme für die Ladung bei 1c immer nur 0 heraus.
Ladungsverteilung der xz Ebene:
\frac{q}{4\pi }\left [\frac{2b}{\sqrt{(x+a)^2 +b^2 +z^2)}^3} -\frac{2b}{\sqrt{(x-a)^2 +b^2 +z^2)}^3}\right ]
Andere Ebene analog. Summation von x und z von 0 nach unendlich wird null. jemand andere vorschläge?
…also mir kommt zwar das selbe endergebnis raus, aber mein zwischenergebnis schaut anders aus, weil ich phi_{0} erst am ende als rb einsetze und dann noch die Orthogonalitätsrelation ausnütze…ich weis zwar nicht wie du auf diese zwischenergebnis kommst…aber bei mir bleibt eine allgemeine konstante da stehen, weil ich die rb phi_{0} noch gar nicht verwendet habe;)…obwohl konstante mal konstante auch konstante ist ![]() …vlg andi
…vlg andi
Anderer Vorschlag: Nochmals in die Angabe schaun ![]()
→ z geht von -unendlich bis +unendlich ![]()
Kann grad nicht wirklich denken … nach ewig Rumgetue kommt mir das gleiche raus, mit A_n = Koeffizienten
Aber wie hast du die bestimmt? Mir bleibt dafür nur die RB phi(y=0) = phi_0 …
2a: Danke an Lelouch; allerdings hab ich es mit genau der Vorgehensweise nicht zusammengebracht, war immer irgendwas falsch … habs mir dann als \frac{d}{dx}P_{n+1}(x) = (2n+1)\frac{d}{dx}P_n(x) + \frac{d}{dx}P_{n-1}(x) angeschrieben, den ^n+1-Term wie beschrieben 2x abgeleitet, das d/dx und den n-1-Term zu d^n/dx^n zusammengefasst, herumgerechnet… dann passts irgendwann
2b: Es gibt eine lustige alternative Darstellung, die man durch Ausmultiplizieren der Rodrigues-Formel erhält:
http://mathworld.wolfram.com/LegendrePolynomial.html
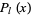
(32)
Für x = 0 ist nur der Summenterm mit x^0 relevant (weil alle anderen eh 0 sind), sodass sich ergibt:
\frac{(-1)^n}{2^{2n}} \begin{pmatrix}2n\n\end{pmatrix} \begin{pmatrix}4n-2n\2n\end{pmatrix} = \frac{(-1)^n}{2^{2n}} \frac{(2n)!}{n!n!} \frac{(2n)!}{(2n)!} = \frac{(-1)^n}{2^{2n}} \begin{pmatrix}2n\n\end{pmatrix}
zum 3er:
Ich habe die randbedingung für phi_0 etwas voreilig eingesetzt gehabt, die brauche ich eigentlich erst wenn ich dann die Fourier-Koeffizienten bestimme aber es ist kein fehler, weil in meinem fall fällt das phi_0 für die A_n einfach raus und andernfalls würds drinnen bleiben.
Falls du das Prama 2 Skript zur hand hast, dort habe ich die formel dafür quasi adaptiert (Seite 84 ab 4.25). Dabei trickst man auch ein wenig. Bei der orthogonal relation führt man das integral mit seiner bisherigen lösung durch und setzt einfach y=0 (dort wo noch die summe unter dem integral steht) so dass dein A_n unter der summe bleibt. da ja nur n=m ungleich 0 wird beim integral fällt die summe weg und das A_n wird zum A_m. dann bei dem ausdruck ganz unten setzt du für deine funktion allerdings die RB an y=0 ein (also Phi_0) und auswerten des integrals liefert die koeffizienten (nicht vergessen zu beachten welche werte m annehmen kann).
1 c und d bekomm ich immer noch nicht auf die reihe, auch wenn ich z richtig von minus unendlich nach unendlich gehen lasse #-o
stimmt denn der ladungsdichte ausdruck den ich weiter oben geschrieben habe? wenn ja kann wer bitte kurz beschreiben wie er das integral gehandhabt hat?
Ein zu Bsp 1 ähnliches Bsp gibts übrigens auf http://www.physik.tu-muenchen.de/lehrstuehle/T30a/vorlesungen/WS0809/uebungen/ed08_3.pdf (Bsp 11) + Lösung http://www.physik.tu-muenchen.de/lehrstuehle/T30a/vorlesungen/WS0809/uebungen/ed08_3Los.pdf
Bsp. 1:
Bsp 1.pdf (1.88 MB)
@rfc822 Die alternative Formel für das Legendre Polynom gibts auch im Wiki, allerdings steht in der Angabe man
soll das ganze mit Hilfe der Rodrigues Formel zeigen. Ankreuzen versuchen kann aber immer.
-
Von welchem Wiki ist die Rede? Und ich bin mir sicher, die Formel gibt’s an anderen Stellen auch noch…
-
Ich hab nie gesagt, dass das Beispiel damit vollständig erledigt ist (obwohl man die alternative Formel auch als Formel von Rodrigues bezeichnen könnte, dann wäre es vollständig).
-
Ich denke mal, dass es der einfachste Weg ist, die Identität von alternativer Formel und Formel aus der Angabe zu zeigen (einfacher als selber abzuleiten, ohne zu wissen was rauskommt). Deswegen ist sie zumindest sicher nützlich. Wer meinen Post nicht lesen will, soll’s halt bleiben lassen…
4tens muss ich vorsichtig formulieren, man weiß ja nicht mit wem man schreibt bzw. wer hier mitliest - aber der Zeitaufwand für die Übung ist meiner Meinung nach absolut lächerlich (im Sinne von: die VU braucht so ziemlich die ganzen Wochenressourcen). Ich mach’s jetzt aus Anrechnungsgründen schon zum 2ten Mal, ich mach sicher keinen Strich mehr zu viel…
Apropos Zeitaufwand: Gibt’s eigentlich schon Testergebnisse?